Kepler's Laws

This lesson covers: 

  1. Understanding Kepler's first law about elliptical orbits with the Sun at one focus.
  2. Exploring Kepler's second law regarding equal areas being swept out in equal times.
  3. Investigating Kepler's third law that links orbital periods and radii.
  4. A practical example calculation using Kepler's third law.
  5. Understanding how Newton's law of gravitation explains atmospheric thickness.

Kepler's first law

Kepler's first law informs us that planets move around the Sun in elliptical paths, with the Sun occupying one of the two special points inside the ellipse, known as a focus.

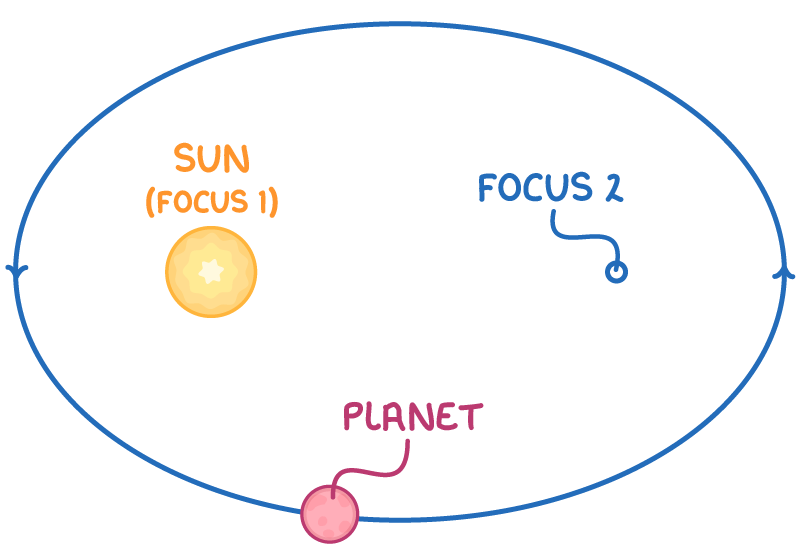
Illustration showing an elliptical orbit with the Sun at one focus and a planet orbiting around it.

This principle is applicable to any smaller body orbiting a larger central object. It's interesting to note that circular orbits are just a specific type of ellipse.

Kepler's second law

Kepler's second law proposes that as a planet orbits the Sun, an imaginary line drawn from the planet to the Sun will cover equal areas in the same amount of time.

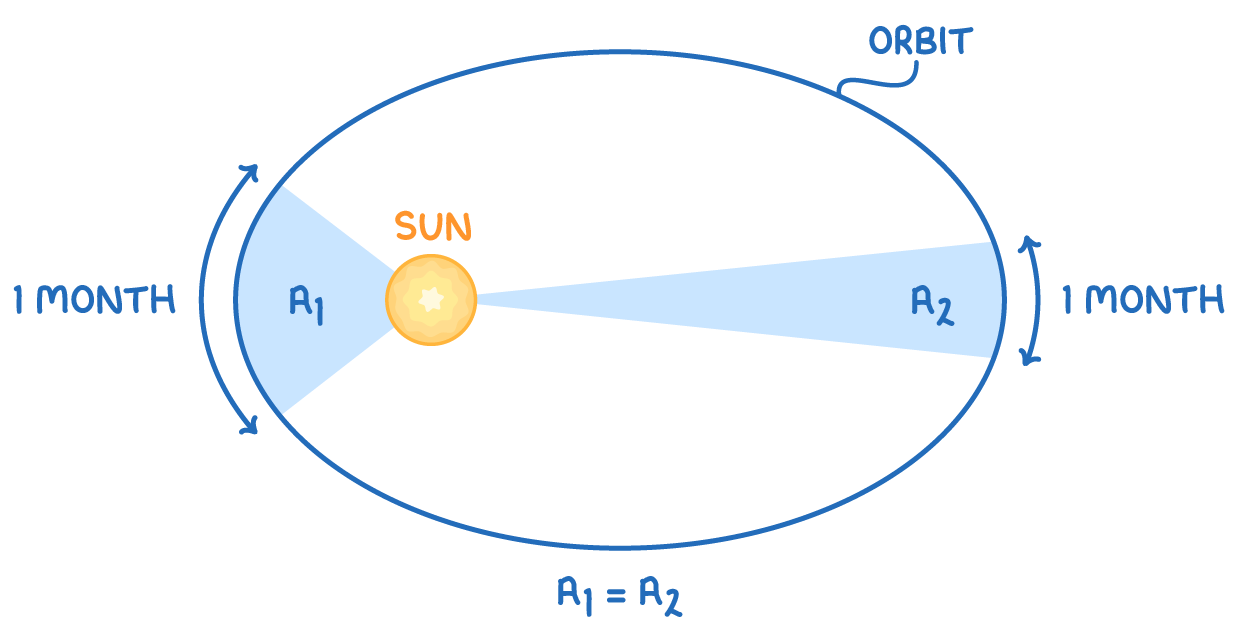
Illustration of Kepler's second law showing a planet's orbit around the Sun with equal areas covered in equal time periods.

This means if a planet travels from point A to B in the same duration it takes to go from C to D, the areas of the two sectors, A-B and C-D, will be equal.

Kepler's third law

Kepler's third law provides a relationship between the time taken for a complete orbit (the orbital period, T) and the average distance of the orbit from the Sun (the radius, r). This is expressed as:


T2∝r3


Where:

  • T = time period (s)
  • r = radius (m)


This implies that planets further away from the Sun have longer orbital periods.

Worked example - Applying Kepler's third law to exoplanets

Consider two exoplanets, A and B, orbiting a star. Exoplanet A completes its orbit in 40 hours and has an orbital radius of 4.02 x 105 km. Exoplanet B has an orbital radius 1.5 times larger than A's. Calculate the orbital period of Exoplanet B.


Step 1: Formula:

The constant of proportionality is the same for both Exoplanets.

rA3​TA2​​=rB3​TB2​​


Step 2: Rearrangement for TB

TB​ = √rA3​TA2​×rB3​​​


Step 3: Calculate orbital radius rB

rB​ = 1.5×4.02×105=6.03×105 km


Step 4: Substitution and correct evaluation

TB​ = √(4.02×105)3402×(6.03×105)3​​ = 73.5 hours

Newton's law of gravitation and atmospheric thickness

Isaac Newton's law of universal gravitation helps explain why planets have atmospheres of varying thickness:

  1. A planet's gravity attracts atmospheric particles, preventing them from escaping into space.
  2. Larger planets have a stronger gravitational pull, effective further from their surface.
  3. As a result, these planets retain more atmospheric particles, leading to thicker atmospheres.