Capacitors In Series & Parallel

This lesson covers: 

  1. How connecting capacitors in parallel increases the total capacitance.
  2. The relationship between individual and total capacitance for capacitors in parallel.
  3. How connecting capacitors in series decreases the total capacitance.
  4. The mathematical relationship between capacitances in a series circuit.

Capacitance increases in parallel

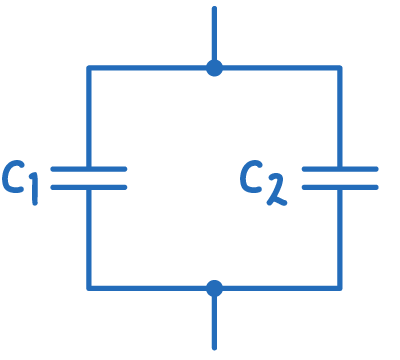
Diagram of a circuit showing two capacitors C1 and C2 connected in parallel.

When capacitors are connected in parallel within a circuit, each one experiences the same potential difference (voltage). The formula for capacitance is given by:


C=VQ​


Where:

  • C = capacitance (F)
  • Q = charge (C)
  • V = potential difference (V)


In a parallel connection, since the potential difference across each capacitor remains constant, the charge Q that each capacitor can store does not change from when it is connected individually. This implies that the total capacitance of capacitors in parallel is the sum of their individual capacitances:


Ctotal​ = C1​+C2​


Where:

  • Ctotal = overall capacitance (F)
  • C1 and C2 = capacitances of the individual capacitors (F)

Worked example - Calculating total capacitance in parallel

Calculate the total capacitance of a circuit that includes two capacitors in parallel, with capacitances of 4 μF and 6 μF.


Step 1: Formula

Ctotal​= C1​+C2​


Step 2: Substitution and correct evaluation

Ctotal​=4×10−6+6×10−6 = 10 μF

Capacitance decreases in series

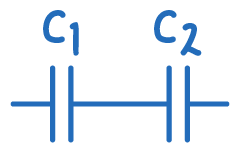
Diagram showing capacitors C1 and C2 connected in series.

Capacitors connected in series within a circuit distribute the total potential difference (voltage) across themselves. This means that each capacitor in a series connection holds the same charge (Q), regardless of its individual capacitance.

The formula for determining the total capacitance of capacitors in series is derived as follows:


Ctotal​1​=C1​1​+C2​1​


Where:

  • Ctotal = overall capacitance (F)
  • C1 and C2 = capacitances of the individual capacitors (F)


This relationship shows that the total capacitance of a series connection is always less than the smallest individual capacitance in the group.

Worked example - Calculating total capacitance in series

Determine the total capacitance of a circuit containing two capacitors connected in series, each with capacitances of 4 μF and 6 μF.


Step 1: Formula

Ctotal​1​=C1​1​+C2​1​


Step 2: Substitution and correct evaluation

Ctotal​1​=4×10−61​+6×10−61​=31,250,000​

Ctotal​=1,250,0003​ = 2.4×10−6 F