Binding Energy

This lesson covers: 

  1. What nuclear binding energy is and how it relates to mass defect.
  2. Calculating nuclear binding energy from mass defect.
  3. Trends in binding energy per nucleon across different nuclei.
  4. Energy released from nuclear fission and nuclear fusion reactions.

Nuclear Binding Energy

The nuclear binding energy is the energy that is required to disassemble a nucleus into its component protons and neutrons.

Nuclei are observed to have a mass that is slightly less than the total mass of their individual protons and neutrons. This difference in mass is known as the mass defect (Δm). The mass defect is converted into energy during the formation of a nucleus, following Einstein's famous equation:


E = Δm c2


Where:

E = energy (J)

Δm = mass defect (kg)

c = speed of light (3 x 108 m s-1)

Worked example - calculating the binding energy of a boron nucleus.

The mass defect for a Boron-11 nucleus is 0.0558 u.

Calculate the binding energy of the boron nucleus in J.


Step 1: Formula

E = Δm c2


Step 2: Convert u into kg

1 u = 1.661 x 10-27 kg.

0.0558 u =9.26838 x 10-29 kg


Step 3: Substitution and correct evaluation

E = 9.26838 x 10-29 x (3x108)2 = 8.34 x 10-12 J

Binding energy per nucleon

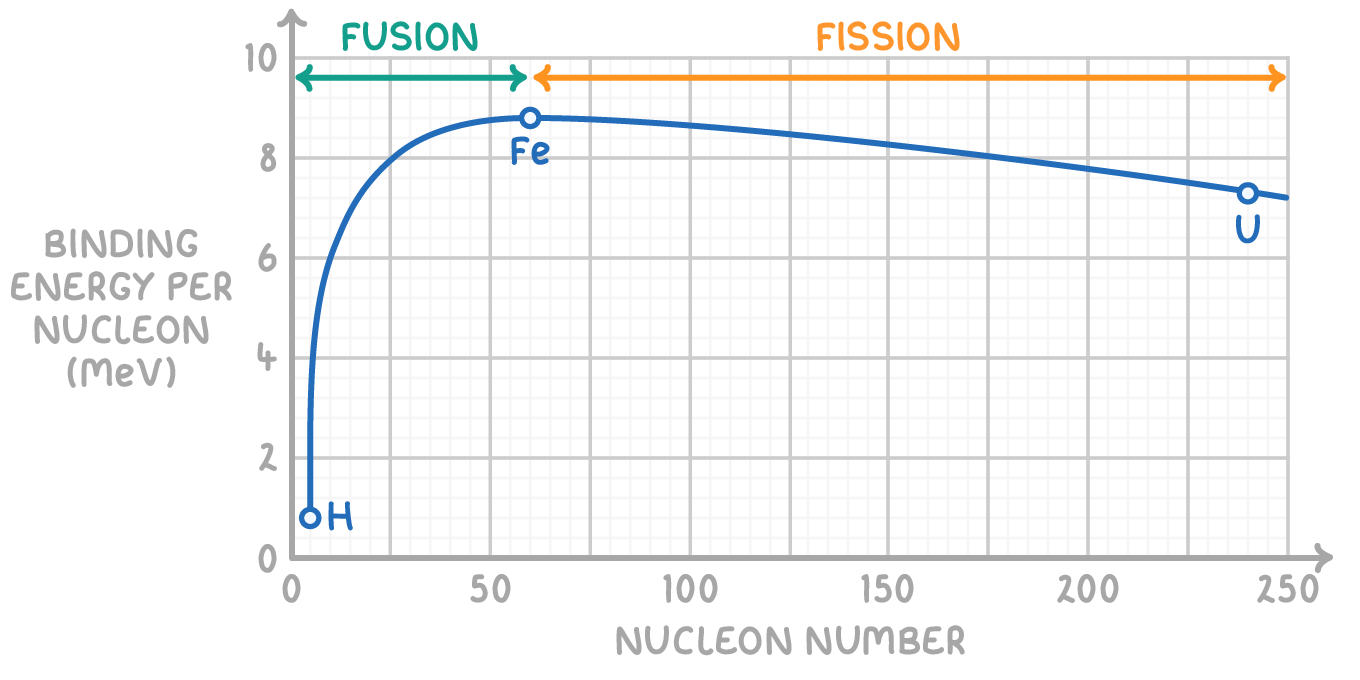
Graph showing binding energy per nucleon in mega electron volts against nucleon number, highlighting areas of fusion and fission.

The concept of binding energy per nucleon is a measure of how tightly bound each nucleon is within the nucleus. It's crucial for understanding the stability of nuclei.

  • Light nuclei exhibit a lower binding energy per nucleon, indicating a weaker hold among nucleons.
  • Conversely, the heaviest nuclei also display a reduction in binding energy per nucleon due to their inherent instability.


Recognising this pattern is essential for predicting the energy released from nuclear fission and fusion reactions.

Worked example: Calculating the binding energy per nucleon for a Lithium nucleus

The mass defect of a Lithium nucleus is 0.04211 u.

Calculate the binding energy per nucleon for the 73Li nucleus in MeV.


Step 1: Formula

E = Δm c2


Step 2: Convert u to kg

1 u = 1.661 x 10-27 kg

0.04211 u = 6.994471 x 10-29 kg


Step 3: Calculate binding energy

E = 6.994471 x 10-29 x (3 x 108)2 = 6.2950239 x 10-12 J


Step 4: Calculate binding energy per nucleon

Lithium has 7 nucleons therefore the binding energy per nucleon is given by:

E = 76.2950239×10−12​=8.99×10−13 J


Step 5: Convert J to MeV

to convert from J to MeV, divide by 1.6 x 10-13

8.99 x 10-13 = 5.6 MeV