Stellar Radii

This lesson covers: 

  1. How hot gases produce line emission spectra
  2. Creating absorption spectra by passing white light through a cool gas
  3. Identifying elements from their spectral lines
  4. Relating a star's luminosity, radius and temperature using Stefan's Law
  5. Using Wien's Displacement Law to link a star's peak wavelength and temperature
  6. Estimating a star's radius by combining Stefan's and Wien's Laws

Hot gases emit line spectra

When a gas is heated to a high temperature, its electrons can move to higher energy levels. As electrons fall back down to lower energy levels, they release energy as photons. The particular energies of the photons depend on the quantised energy level transitions in that element.

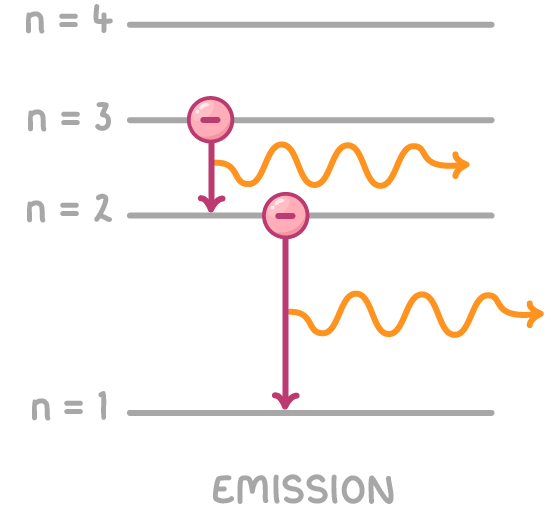
Diagram showing electrons falling to lower energy levels and emitting photons, illustrating the emission line spectrum.

This one was drawn for 2.02 but we only need the emission side for this one.

If this light is passed through a diffraction grating, the result is a line emission spectrum - a series of sharp, coloured spectral lines against a dark background. Each coloured line corresponds to a particular wavelength of light.

  • Emission lines are quantised and element-specific, allowing identification of gases
  • Line positions can be used to calculate photon energies using diffraction grating equation

Absorption spectra from white light

A line absorption spectrum is produced when white light passes through a cool, low-pressure gas.

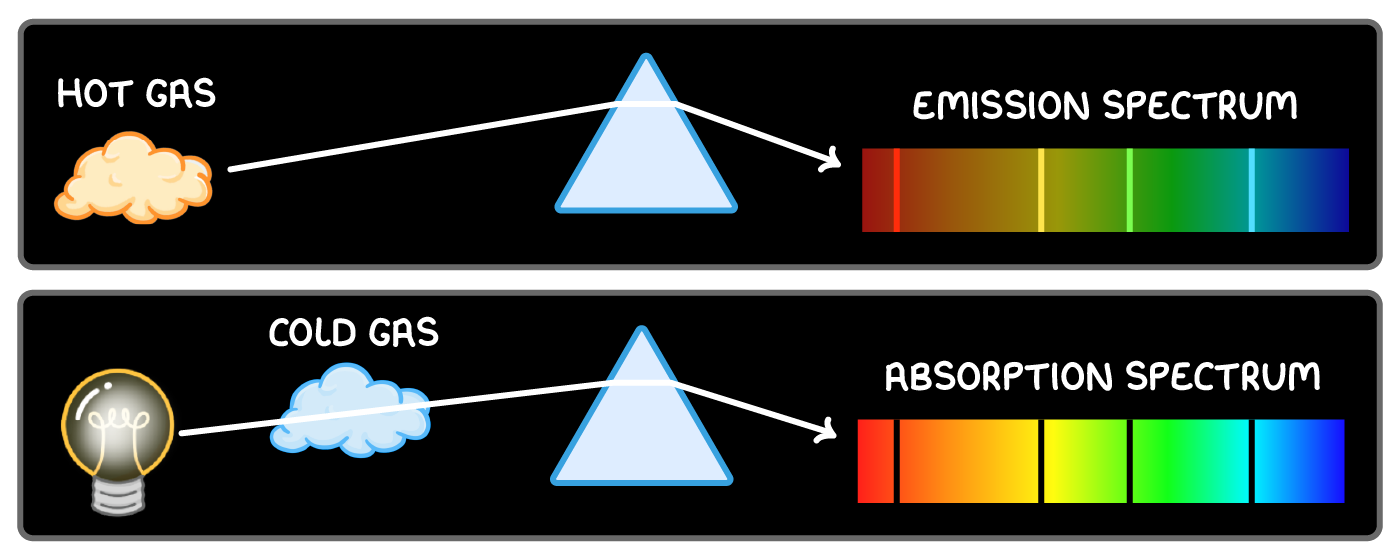
Diagram showing the difference between emission and absorption spectra with hot gas and cold gas.
  • At lower temperatures, most electrons occupy ground state
  • Photons of specific wavelengths are absorbed, exciting electrons up to higher levels
  • Missing wavelengths appear as dark lines against the continuous spectrum


Emission and absorption spectra are complementary - absorption lines align with emission lines. This allows identification of elements.

Stellar absorption spectra occur due to starlight passing through outer gas layers. Comparing absorption lines with laboratory spectra enables stellar composition analysis.

Relating luminosity, radius and temperature

A star's luminosity (L) is its total power output. Stefan's Law gives:


L=4πR2σT4


Where:

  • L = Luminosity (W)
  • R = Radius (m)
  • σ = Stefan-Boltzmann constant (5.67 x 10-8 W m-2 K-4)
  • T = Surface temperature (K)

Worked example - Estimating the radius of Betelgeuse

Betelgeuse has a luminosity of 1.2 x 1031 W and a peak wavelength of 970 nm. Calculate the radius of Betelgeuse.


Step 1: Convert nm to m

to convert from. nm to m, multiply by 1 x 10-9

970 nm = 970 x 10-9 m


Step 2: Wien's law formula

λmax​T=2.9×10−3


Step 3: Rearranged formula

T=λmax​2.9×10−3​


Step 4: Substitution and correct evaluation

T=970×10−92.9×10−3​=2989.7 K


Step 5: Stefan’s law formula

L=4πR2σT4


Step 6: Rearranged formula

R=√4πσT4L​​


Step 7: Substitution and correct evaluation

R=√4π×5.67×10−8×(2989.7)41.2×1031​​ = 4.6 x 1011 m