Simple Harmonic Systems

This lesson covers: 

  1. Understanding mass-spring systems as simple harmonic oscillators
  2. Exploring Hooke's law and the restoring force exerted by springs
  3. The equations for frequency and period of a mass on a spring
  4. Introducing the simple pendulum as another example of a simple harmonic oscillator
  5. Analysing the forces acting on a pendulum bob and equations for a simple pendulum

The mass-spring system

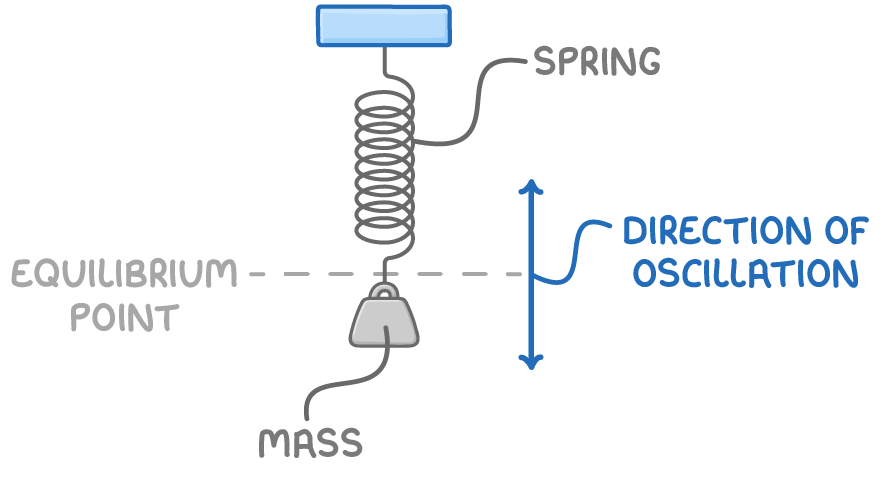
Diagram of a mass-spring system showing the mass, spring, equilibrium point, and direction of oscillation.

A mass-spring system is a classic example of a simple harmonic oscillator (SHO). In this system, when a mass attached to a spring is displaced from its equilibrium, or rest, position, the spring exerts a force to return the mass to its original position.


This force, known as the restoring force, is proportional to the displacement and is described by Hooke's law:


F = − k x


Where:

  • F = restoring force in newtons (N)
  • k = spring constant in newtons per metre (N m-1)
  • x = displacement from equilibrium in metres (m)


The negative sign in the equation indicates that the force acts in the opposite direction of the displacement, aiming to restore equilibrium.

Applying Newton's laws

When we apply Newton's second law of motion, we obtain an expression for the angular frequency of the oscillator:


ω2=mk​


Substituting ω for T2π​ gives:

(T2π​)2=mk​


T = 2π√km​​


Where:

  • T = time period (s)
  • m = mass (kg)
  • k = spring constant (N m-1)


A higher spring constant or a lower mass results in a greater frequency and a shorter period.

Worked example - Calculating the frequency of a mass-spring system

Calculate the time period of a mass-spring system with a mass of 0.5 kg and a spring constant of 200 N m-1.


Step 1: Formula

T = 2π√km​​


Step 2: Substitution and correct evaluation

T = 2π√2000.5​​ = 0.31 s

The simple pendulum

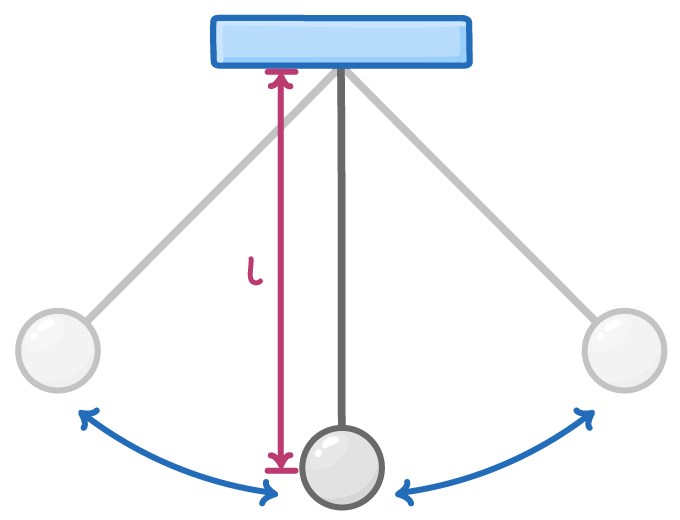
Diagram showing the motion of a simple pendulum with a mass hanging from a string and the forces acting on it.

A simple pendulum, which consists of a mass hanging from a string, also acts as a simple harmonic oscillator. The forces responsible for the pendulum's motion are gravity, pulling the mass downwards, and the tension in the string, which provides the restoring force.


The period of a simple pendulum is given by:


T=2π√gL​​


Where:

  • T = time period in seconds (s)
  • L = length of the pendulum in metres (m)
  • g = acceleration due to gravity (9.81 m s-2)


Note: changing the mass of the pendulum bob has no effect on the tie period of the pendulum.

Worked example - calculating the period of a simple pendulum

Let's calculate the period of a simple pendulum with a length of 2 meters, assuming an acceleration due to gravity (g) of 9.81 m s-2.


Step 1: Formula

T=2π√gL​​


Step 2: Substitution and correct evaluation

T=2π√9.812​​ = 2.84 s

Applying simple harmonic motion concepts

Simple harmonic motion is a concept that extends beyond mass-spring systems and pendulums.


It applies to various oscillating systems such as:

  • Water oscillating in U-tubes
  • Alternating current (AC) circuits with inductors and capacitors
  • Vibrating strings and air columns


In each case, the period of oscillation depends on the specific properties of the system, but the motion typically follows a sine or cosine function.