Moving Charges In A Magnetic Field

This lesson covers: 

  1. The force experienced by charged particles in magnetic fields
  2. How magnetic fields affect current in wires through acting on electrons
  3. Determining the force on a single charged particle from the magnetic force equation
  4. The deflection of charged particles into circular paths inside magnetic fields
  5. Using magnetic and electric fields in velocity selectors

Forces act on charged particles in magnetic fields

Electric current in a wire results from negatively charged electrons moving through the wire. Since electrons are charged particles, they experience forces when inside magnetic fields.


The magnetic force equation for current-carrying wires perpendicular to a magnetic field is:


F = B I l


Where:

  • F = Magnetic force (N)
  • B = Magnetic field strength (T)
  • I = Current (A)
  • l = Length of wire in field (m)

Force on a single charge

This equation can be adapted to describe the force on individual charges:

Diagram showing an electron moving through a magnetic field directed into the page, with the resulting force perpendicular to its motion.

As seen in the previous section, the force experienced by a current carrying conductor is given by:


F = B I l


Since current is the rate of flow of charge, the equation becomes:


F = tB Q l​


Distance (l) over time (t) is equal to velocity (v), therefore the force on a single charge becomes:


F= B Q v


Where:

  • B = Magnetic field strength (T)
  • Q = charge (C)
  • v = velocity (m s-1)


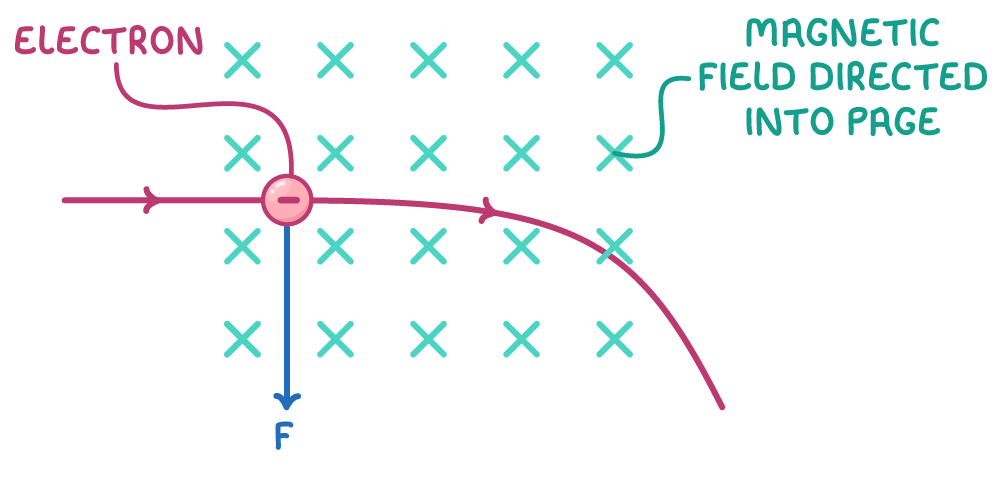
So a magnetic field exerts a force perpendicular to the motion of charges inside it.

Worked example - Calculating the force on a charge moving through a magnetic field

A proton moves at a velocity of 3.0×106 m s−1 perpendicular to a magnetic field of strength 0.5 T. Calculate the force experienced by the proton.


Step 1: Formula

F = B Q v


Step 2: Substitution and correct evaluation

F=0.5×1.6×10−19×3.0×106=2.4×10−13 N

Circular motion of charged particles

The perpendicular magnetic force causes charged particles to follow curved paths inside the field.


By Fleming's left hand rule, the force is always perpendicular to the particle's velocity. So the magnetic force provides the centripetal force for circular motion:


Fc​=rm v2​


Where:

  • m = Mass (kg)
  • v = Velocity (m s-1)
  • r = Radius (m)


Equating magnetic and centripetal forces:


B Q v=rm v2​


The radius of curvature can be expressed as:

r = B Qm v​

Worked example - Determining the radius of curvature for an electron in a magnetic field

An electron enters a magnetic field of strength 1.0 T at a velocity of 2.0 x 107 m s-1.

Calculate the radius of the electron's path within the field.

electron mass = 9.11 x 10-31 kg.

electron charge = -1.6 x 10-19 C.


Step 1: Formula

r = B Qm v​


Step 2: Substitution and correct evaluation

r=1.0×−1.6×10−199.11×10−31×2.0×107​ = 1.14 x 10−4 m

Velocity selectors

Velocity selectors use this principle, employing magnetic and electric fields to filter particles by speed.

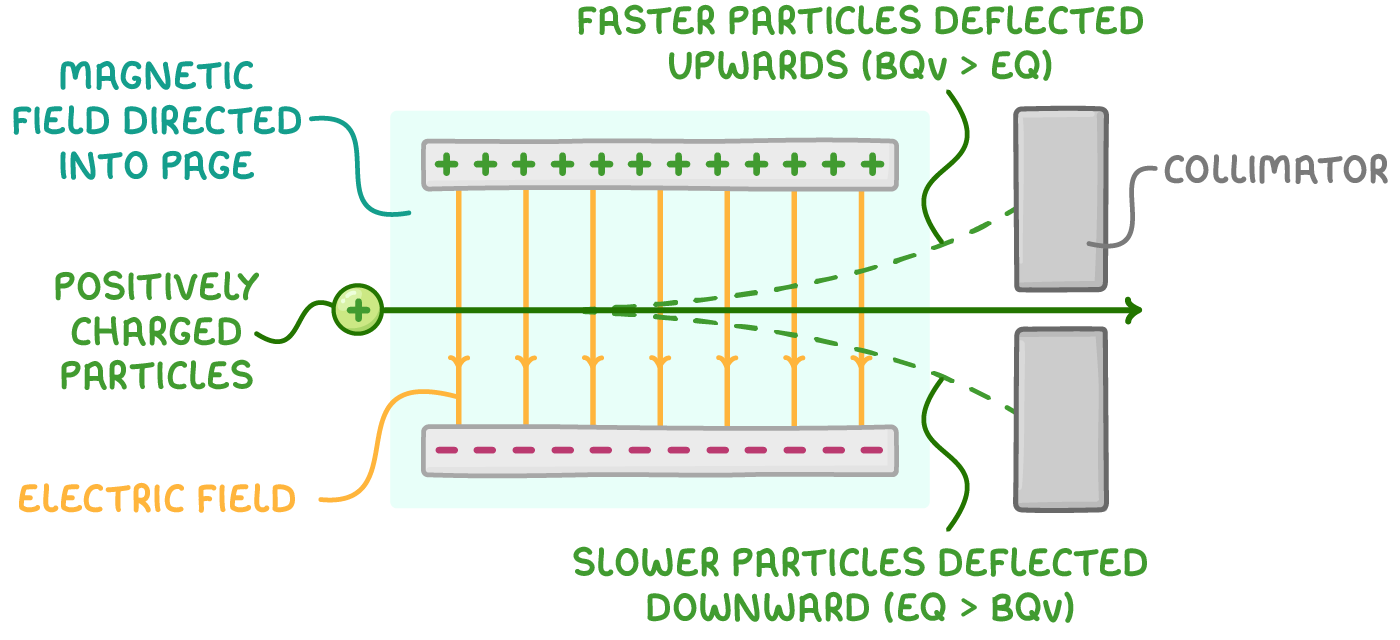
Diagram showing how a velocity selector uses perpendicular electric and magnetic fields to filter particles by speed, with faster particles deflected upwards and slower particles deflected downwards.

Velocity selectors have:

  • Perpendicular electric (E) and magnetic (B) fields
  • Stream of particles with range of speeds
  • Collimator - narrow opening for selected particles


How it works:

  1. The magnetic field is directed into the page and deflects positively charged particles upwards. The force experienced by these charged particles due to the magnetic field is given by:


F= B Q v


  1. The electric field is perpendicular to the magnetic field and is directed top to bottom. The force experienced due to the electric field is given by:


F = E Q


  1. When the magnetic field and electric field forces are the same, the particles will travel through the velocity selector undeflected. The velocity of the selected particle is given by:


B Q v = E Q


B v = E


v = BE​


Velocity selectors can filter a range of charges to select those at a desired speed v. The selected velocity v depends on E and B, which can be varied.

Worked example: - Using a velocity selector

A velocity selector has an electric field strength E=2.0×103 V m−1 and a magnetic field strength B=0.01 T. Calculate the velocity of the particles that pass through undeflected.


Step 1: Formula

v = BE​


Step 2: Substitution and correct evaluation

v = 0.012.0×103​=2×105 m s−1