Simple Harmonic Motion
This lesson covers:
- The definition of simple harmonic motion (SHM) in relation to acceleration and displacement
- How to represent displacement, velocity, and acceleration in SHM through graphs
- The independence of frequency and period from amplitude in SHM
- Essential equations pertinent to SHM
Definition of simple harmonic motion
The acceleration of the object is proportional to the displacement and acts in the opposite direction to the displacement.
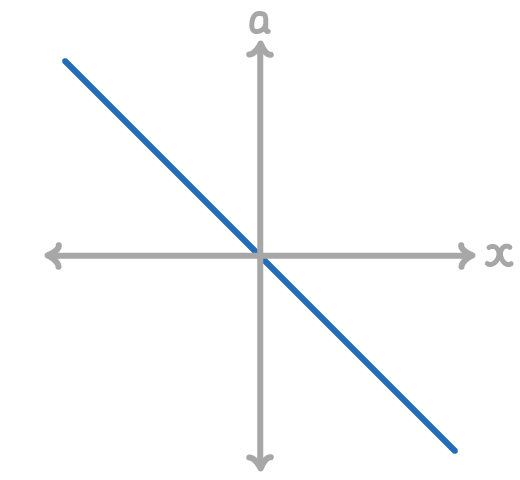
The negative gradient shows that the acceleration is always directed towards the equilibrium point position.
The acceleration in Simple harmonic motion is related to the displacement by the equation:
a = −ω2x
Where:
- ω = angular frequency (rad s-1)
- x = displacement from the midpoint (m)
Displacement during SHM
The variation of displacement with time can be plotted to show a sinusoidally repeating graph:
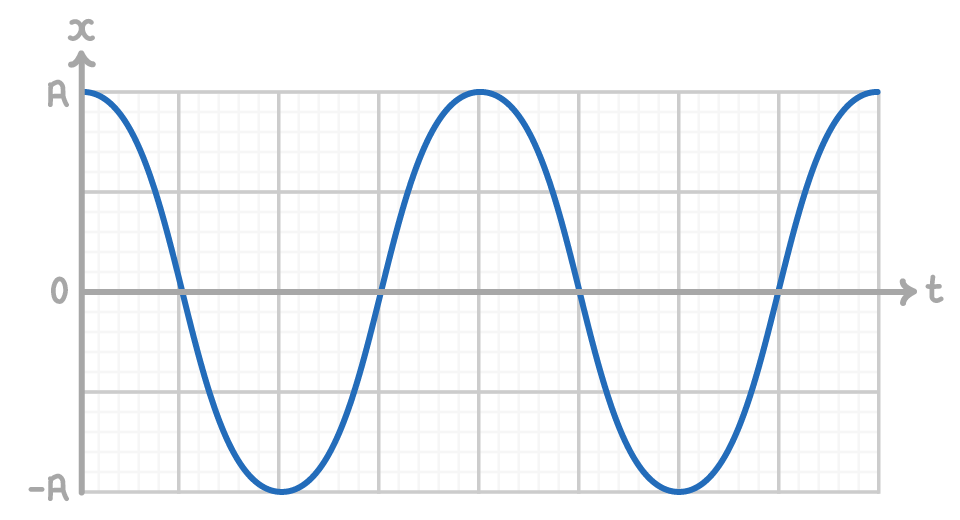
The displacement can be expressed in terms of amplitude, angular velocity and time:
x = A cos(ωt)
Where:
x = displacement (m)
A = amplitude (m)
ω = angular frequency (rad s-1)
t = time (s)
Velocity during SHM
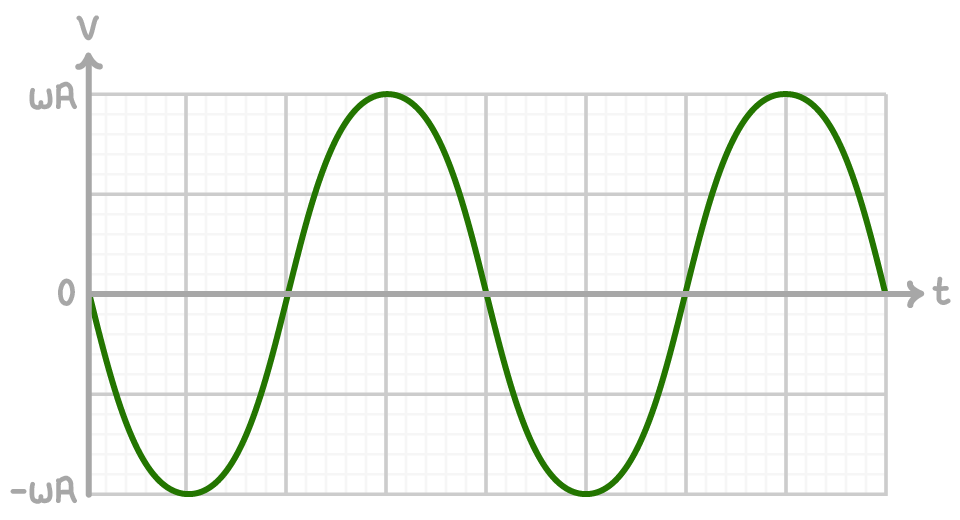
Velocity is 90° out of phase with displacement during simple harmonic motion.
- velocity is maximum when displacement is zero
- velocity is zero when the displacement is maximum
The velocity is related to the angular speed, displacement and amplitude by:
v = ±ω√A2−x2
Where:
v = velocity (m s-1)
ω = angular frequency (rad s-1)
A = amplitude (m)
x = displacement (m)
The maximum velocity occurs when the displacement is zero:
vmax = ω A
Acceleration
Acceleration is 180° out of phase with displacement during simple harmonic motion.
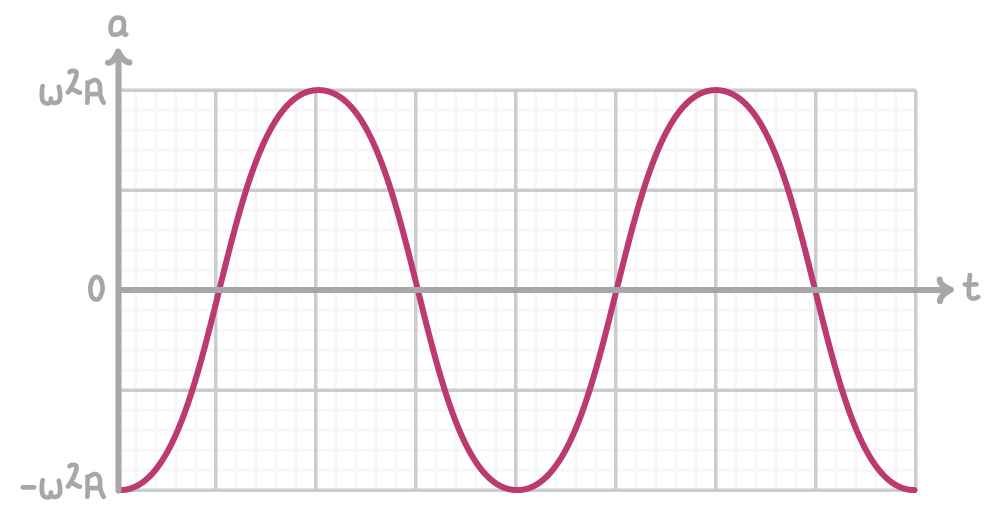
The maximum acceleration occurs when displacement is equal to the amplitude:
amax = ω2 A
Where:
a = acceleration (m s-2)
ω = angular frequency (rad s-1)
A = amplitude (m)
Worked example - Determining maximum velocity in simple harmonic motion
Calculate the maximum velocity of an object undergoing SHM with an amplitude of 0.5 m.
The angular frequency is 10 rad s-1.
Step 1: Formula
vmax = ω A
Step 2: Substitution and correct evaluation
vmax = ω A = 10 × 0.5 = 5 m s−1