Centripetal Force & Acceleration

This lesson covers: 

  1. Understanding how objects moving in circular paths have changing velocity vectors
  2. Defining centripetal acceleration and the methods used to calculate it
  3. Explaining centripetal forces and their role in producing circular motion
  4. An experiment to explore centripetal motion using a whirling bung

Circular motion involves changing velocity

When an object moves along a circular path at a constant speed, its velocity vector changes direction continuously.

Acceleration is defined as the rate of change in velocity. Therefore, even if the speed remains constant in circular motion, the object accelerates because the direction of its velocity changes.

This acceleration, which is always directed towards the centre of the circle, is known as centripetal acceleration (ac).

Calculating centripetal acceleration

To calculate centripetal acceleration, you can use two fundamental equations:


ac​ = rv2​


AND


ac​ = ω2 r


Where:

  • ac = centripetal acceleration (measured in metres per second squared, m s-2)
  • v = linear velocity (m s-1)
  • ω = angular velocity (rad s-1)
  • r = radius of the circular path (m)

Worked example - Calculating centripetal acceleration

Calculate the centripetal acceleration for a car moving at 20 m s-1 around a circular track with a radius of 50 metres.


Step 1: Formula

ac​ = rv2​


Step 2: Substitution and correct evaluation

ac​=50202​ = 40 m s−2

Centripetal forces cause circular motion

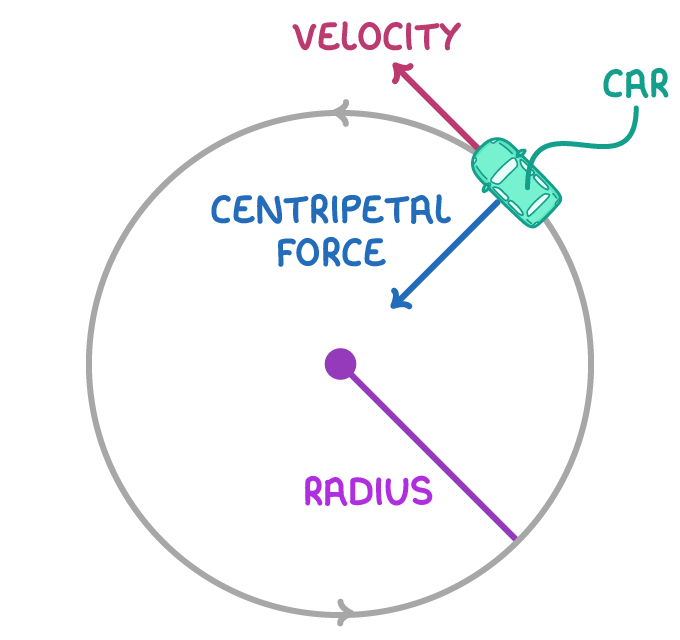
Diagram showing a car moving in a circular path with labels for velocity, centripetal force, and radius.

According to Newton's first law, any accelerating object must experience a net force.

The net force that causes circular motion is called the centripetal force (Fc). This force always points towards the centre of the circle.


Using the formula F = ma, we derive the equations for centripetal force:


Fc​ = rm v2​


AND


Fc​ = m ω2 r


Where:

  • Fc = centripetal force (N)
  • m = mass (kg)
  • v = linear velocity (m s-1)
  • r = radius (m)
  • ω = angular velocity (rad s-1)

Investigating centripetal motion

We can experimentally study circular motion using a whirling bung setup:

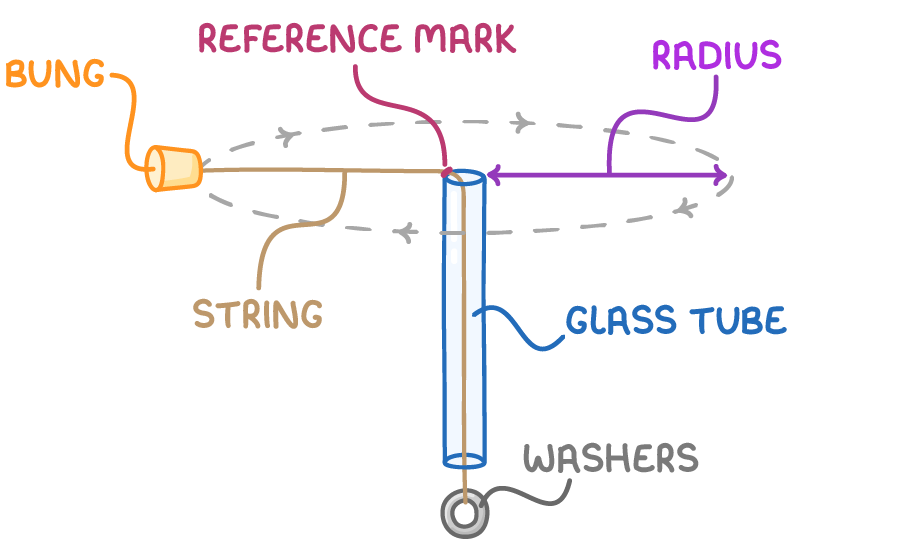
Diagram showing a whirling bung setup with a glass tube, string, washers, and reference mark for investigating centripetal motion.

Method:

  1. Attach some washers to a rubber bung tied to a string, which is threaded through a glass tube.
  2. Spin the bung horizontally while keeping a reference mark on the string at the top of the tube.
  3. Time how long it takes for the bung to complete several revolutions to calculate the angular velocity.
  4. Calculate the centripetal force using the weight of the washers.
  5. Repeat the experiment with different string lengths (radii).


Increasing the radius leads to longer revolution times while maintaining the same centripetal force.

This experiment demonstrates how the tension force in the string acts as the centripetal force, enabling circular motion.