Young Modulus

This lesson covers: 

  1. Defining tensile stress and strain
  2. The ultimate tensile strength and breaking stress of materials
  3. Calculating elastic potential energy stored in stretched materials
  4. Introducing Young's modulus
  5. Experimental methods for determining Young's modulus

Stress and Strain in materials


Diagram showing compressive force and tensile force acting on a material.

Materials deform when external forces are applied to them. These forces can either stretch (tensile force) or squash (compressive force) the material. 

Stress (σ\sigma):

Stress is defined as the force per unit area applied to the material. 


σ = FA\sigma\text{ = }\frac{\text{F}}{\text{A}}


Where:

F = Force applied (N)

A = Cross-sectional area (m2)

Strain (ϵ\epsilon):

Strain is defined as the ratio of a material's deformation to its original length. 


ϵ = xl\epsilon\text{ = }\frac{x}{l}


Where:

x = extension (m)

l = original length (m)

Ultimate Tensile Strength

Graph showing the relationship between stress and strain with a marked point indicating ultimate tensile strength.

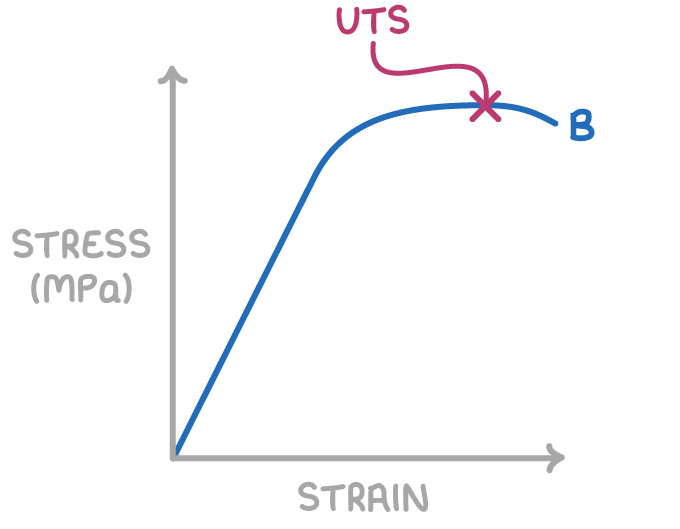
Materials will break under sufficiently high tensile forces.

This breaking point is defined by two key terms:

  • Ultimate tensile strength (UTS) - This is the maximum stress a material can withstand before it breaks.
  • Breaking stress - The stress level at which a material fractures.


UTS values are crucial for engineers designing safe structures.

Elastic Potential Energy

When materials deform, they store energy. This stored energy is known as elastic potential energy.

For a force (F) causing an extension (x), the elastic potential energy is calculated as:

  • Work done = average force x extension = 2F​×x
  • Elastic potential energy (E) = 2Fx​

Worked example - Calculating elastic potential energy in a stretched spring

A spring is stretched by 4 cm using a force of 20 N. Calculate the elastic potential energy stored in the spring.


Step 1: Formula

E = 2Fx​


Step 2: Convert cm to m

to convert from cm to m, divide by 100

4 cm = 0.04 m


Step 3: Substitution and correct evaluation

E = 220×0.04​ = 0.4 J

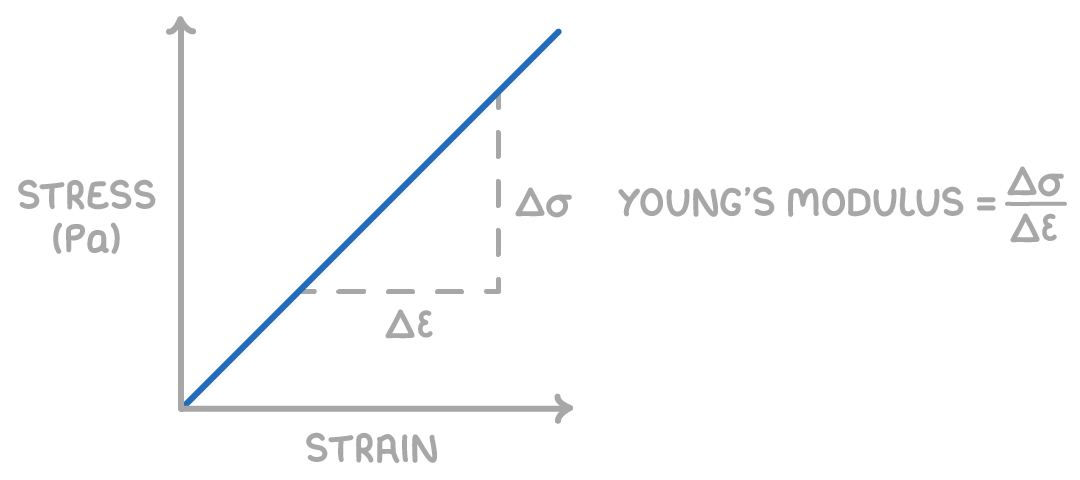
Young's Modulus

Young's modulus is the ratio of stress to strain, and it's constant up to the material's limit of proportionality.


E=ϵσ​=A xF l​


Where:

E = Young's modulus (N m−2)

F = applied force (N)

A = cross-sectional area (m2)

l = original length (m)

x = extension (m)


Young's modulus indicates how stiff a material is, helping engineers choose materials capable of withstanding certain stresses.

Determining Young's Modulus Experimentally

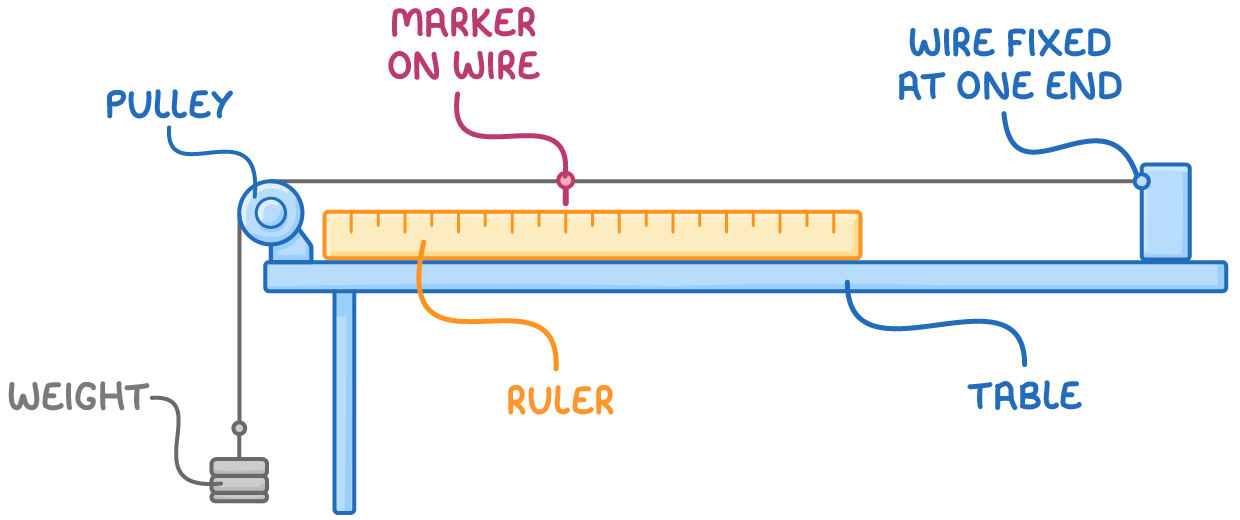
Diagram showing the setup for determining Young's modulus with a wire fixed at one end, a weight on the other, a ruler, and a pulley.

To find Young's modulus, stress-strain data for an extending wire is plotted.

Method:

  1. Attach a thin wire sample of known length (l) and cross-sectional area (A).
  2. Gradually add weights to the wire.
  3. Measure the extension distance (x) for each weight.
  4. Calculate stress (σ) and strain (ϵ) values.
  5. Plot the stress-strain data.
  6. The gradient of the linear part equals Young's modulus (E).
Graph showing stress versus strain with a linear relationship representing Young's modulus.

Worked example - Determining Young's modulus for a material

A 2-meter long wire with a cross-sectional area of 1 x 10-4 m2 stretches by 1 cm under a force of 1,000 N. Calculate Young's modulus for this material.


Step 1: Formula for Young's modulus

Youngs modulus (E) =ϵσ​=AxFl​


Step 2: Convert cm to m

to convert from cm to m, divide by 100

1 cm = 0.01 m


Step 3: Calculate stress (σ)

σ=AF​=1×10−41000​=10×106


Step 4: Calculate strain (ε)

ϵ=lx​=20.01​=5×10−3


Step 5: Calculate Young's modulus (E)

E=ϵσ​=5×10−310×106​=2×109 Pa = 2 GPa