Red Shift
This lesson covers:
- Understanding the Doppler effect for sound waves
- Explaining the Doppler effect using wave diagrams
- Defining red shift and blue shift for light waves
- Using the Doppler effect equation to calculate velocity
- Measuring red shift of stars using absorption spectra
- Describing cosmological red shift
The doppler effect with sound
The doppler effect refers to the change in frequency or wavelength of a wave in relation to an observer when the source of the wave moves towards or away from the observer.
This effect is easily observed with sound waves. For instance, as a police car with its siren on comes closer, the sound's frequency appears higher. Conversely, as it moves away, the frequency lowers.

This phenomenon occurs because:
- The sound waves are compressed in front of the moving source, leading to them being closer together.
- Behind the source, the waves are stretched out, spreading further apart.
The magnitude of this effect increases with the source's speed.
Explaining the Doppler effect
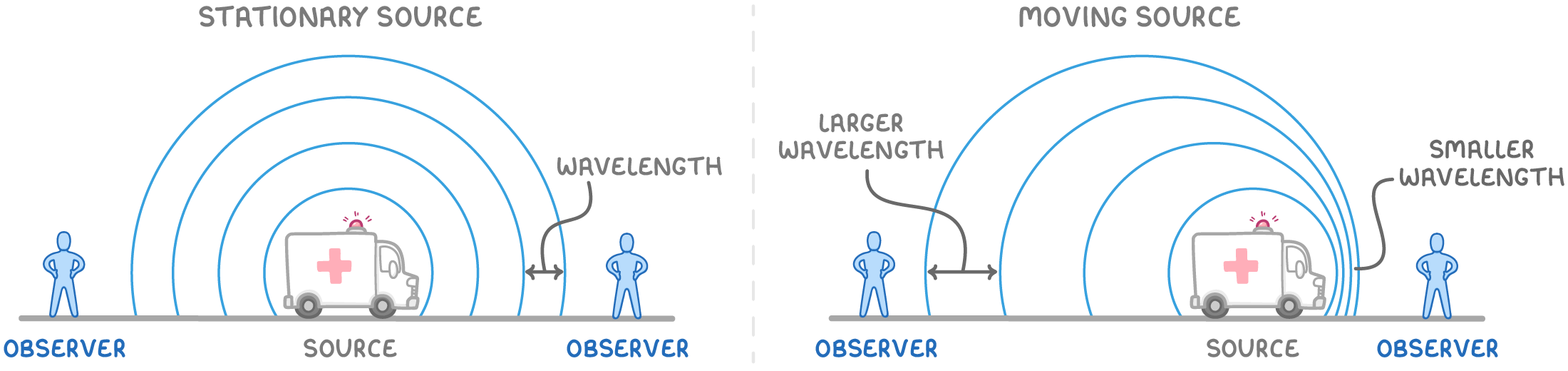
With a stationary source, sound waves emit in evenly spaced concentric circles.
In contrast, a moving source causes the waves to:
- Condense in the direction it is moving towards.
- Disperse in the direction it is moving away from.
This alteration in wavelength happens as the source emits each wave crest from a progressively different location.
As the source nears the observer, the subsequent wave crests have a shorter distance to cover, leading the observer to perceive a higher frequency and shorter wavelength sound.
Light waves and doppler shifts
The Doppler effect also applies to light waves. However, instead of frequency changes manifesting as higher or lower pitches, they result in a colour shift in the light spectrum.
If a light source is moving away, its waves elongate, shifting the colour towards the red part of the spectrum, known as a red shift. This indicates the source's recession.
On the other hand, if the source is approaching, the waves compress, causing the light to shift towards the blue spectrum, termed a blue shift.
For minor velocities, the red shift formula is used:
z=cv
Where:
- z = represents the red shift
- v = source's velocity (m s-1)
- c = speed of light (m s-1)
A positive (v) leads to a positive (z), indicating a red shift; a negative (v) results in a negative (z), indicating a blue shift.
This equation is applicable across all electromagnetic waves. Shifts towards longer wavelengths are universally termed as red shifts, irrespective of their position in the spectrum.
Worked example: - Calculating velocity using the red shift formula
Determine the velocity of a galaxy moving away from Earth, given an observed red shift, (z), of 0.05.
Step 1: Formula
z=cv
Step 2: Rearrangement
v=z×c
Step 3: Substitution and correct evaluation
v = 0.05 x 3 x 108 = 1.5 x 107 m s-1
Measuring a star's red shift
The recessional velocity of a star can be deduced from the red shift observed in its spectrum's absorption lines.
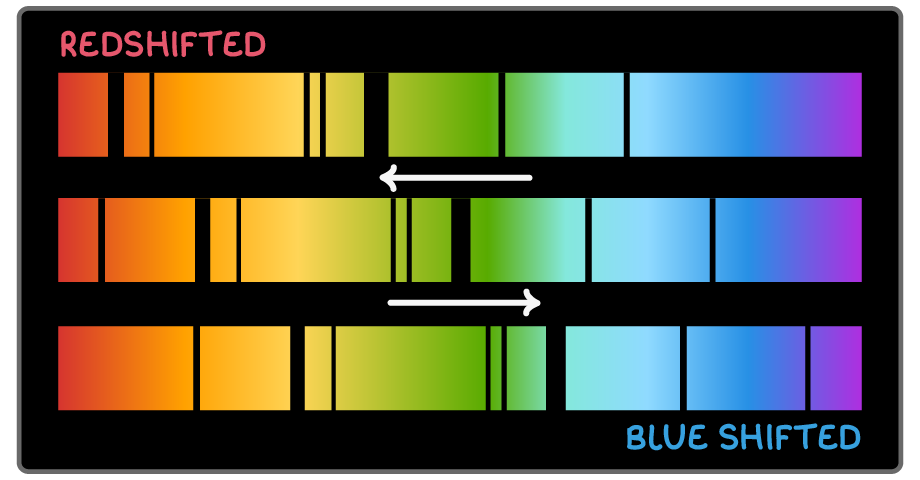
The method involves:
- Comparing the observed wavelength of light with the known wavelength for the same atom or molecule.
- Utilising the red shift formula to correlate the change in frequency/wavelength to velocity.
Cosmological red shift
- Astronomers find that distant galaxies uniformly exhibit red shift. This is not due to their actual motion but indicates the expansion of the universe over time.
- As the fabric of space expands, the wavelengths of light traversing it also stretch, resulting in the observed red shift. This effect is known as cosmological red shift.
- The Doppler formula remains valid for velocities significantly lower than the speed of light. For greater velocities, the principles of relativity are applied.