Experimental Gas Laws
This lesson covers:
- Boyle's Law relating pressure and volume
- Charles' Law relating volume and temperature
- The Pressure Law relating pressure and temperature
- Graphical representations of each gas law
- An experiment to demonstrate Boyle's Law
- An experiment to estimate absolute zero based on the Pressure Law
The Three Gas Laws
These three fundamental gas laws describe how gases behave under various conditions of pressure, volume, and temperature:
- Boyle's Law: This law states that at a constant temperature, the pressure (p) and volume (V) of a gas are inversely proportional to each other.
- Charles' Law: Here, at a constant pressure, the volume (V) of a gas changes in direct proportion to its absolute temperature (T).
- The Pressure Law: This law indicates that at a constant volume, the pressure (p) of a gas is directly proportional to its absolute temperature (T).
An ideal gas perfectly follows these three laws under all conditions.
Boyle's Law - Pressure and Volume Relationship
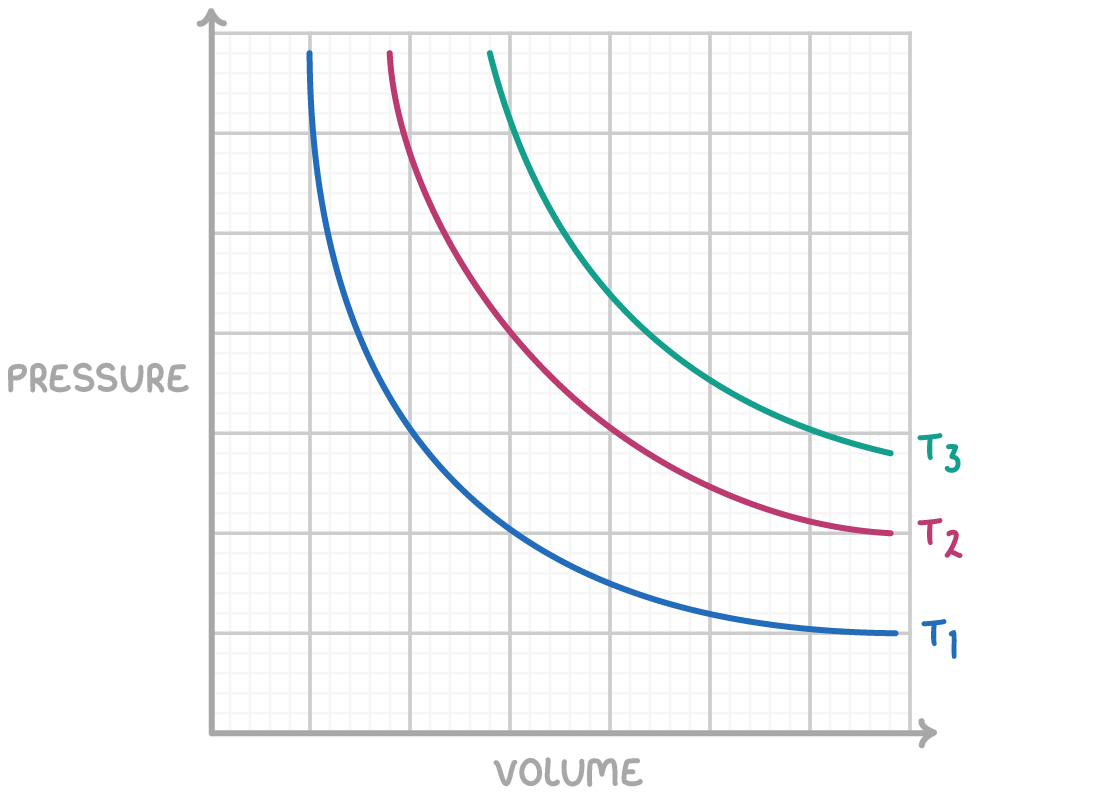
Boyle's Law asserts that for a given amount of gas at a constant temperature:
p V = constant
Where:
- p = pressure (Pa)
- V = volume (m3)
This implies that if the volume increases, the pressure decreases, and vice versa. This inverse relationship is represented graphically as a hyperbola.
Boyle's law experiment
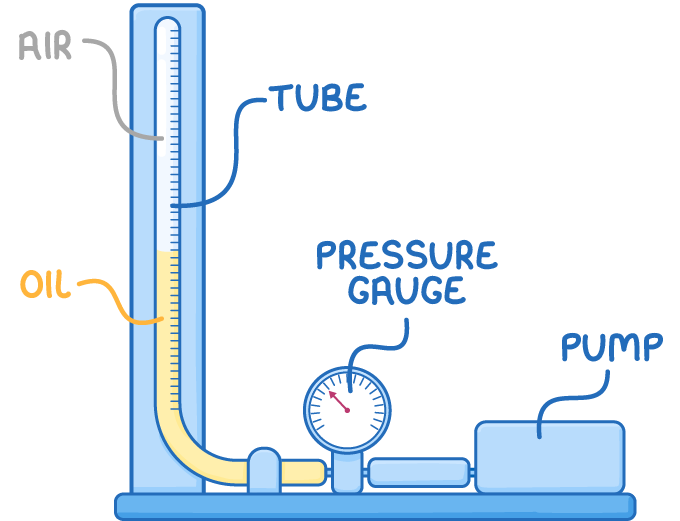
To demonstrate Boyle's Law, you can:
- Confine air in a tube filled with oil.
- Record the initial volume and pressure.
- Calculate the initial product of pressure and volume.
- Use a pump to increase the pressure inside this tube.
- Record the new values for pressure and volume.
- Calculate the new product of pressure and volume.
- If the product calculated initially is equal to the final product, the gas is obeying Boyle's law.
Worked example - Demonstrating Boyle's law with a syringe
Air in a syringe is compressed from 20 cm³ to 10 cm³. The initial pressure is 101 kPa. Calculate the final pressure of the gas after it is compressed.
Step 1: Boyle's law formula
p1V1 = p2V2
Step 2: Substitution and correct evaluation
p2=V2p1V1=10101,000×20=202 kPa
The pressure law - pressure and temperature relationship

The Pressure Law establishes a direct relationship between the pressure (p) and absolute temperature (T) of a gas when the volume is constant:
Tp = constant
Where:
- p = pressure (Pa)
- T = absolute temperature (K)
This indicates a direct proportionality between temperature and pressure under constant volume conditions.
Pressure law experiment

To experimentally verify the pressure law:
- Place an air-filled flask in a temperature-controlled water bath.
- Record the initial temperature and pressure.
- Heat or cool the water, while recording the pressure and temperature changes.
- Plot these changes on a graph of pressure vs. temperature.
- Extrapolate the line to find where it intersects the x-axis, which provides an experimental value for absolute zero.
Worked example - Applying the pressure law in a tyre
A car tyre has a pressure of 202 kPa at 15°C. Calculate the pressure in the tyre if the temperature increases to 35°C.
Step 1: Pressure law formula
T1p1=T2p2
Step 2: Convert celsius to kelvin
to convert from °C to K, add 273.15
T1 = 288.15 K
T2 = 308.15 K
Step 3: Substitution and correct evaluation
p2=p1×T1T2 = 202,000 ×288.15308.15=216 kPa
Charles' law - Volume and temperature relationship
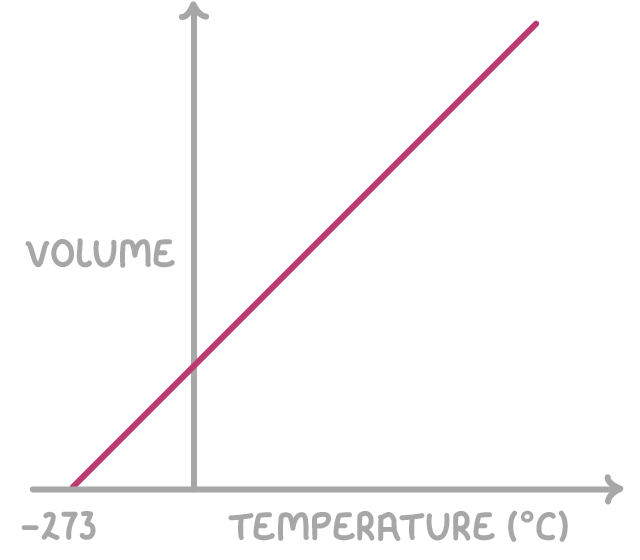
Charles' Law proposes that at a constant pressure, the volume (V) and the absolute temperature (T) of a gas are directly proportional:
TV = constant
Where:
V = volume (m3)
T = temperature (K)
Worked example - Applying Charles' law in a balloon
A helium balloon contains
A helium-filled balloon has a volume of 1 x 10-3 m3 at 20°C.
Calculate the volume of the helium when the temperature is increased to 50°C.
Step 1: Charles' law formula
T1V1=T2V2
Step 2: Convert celsius to kelvin
to convert form °C to K, add 273.15
20°C = 293.15 K
50°C = 323.15 K
Step 3: Substitution and correct evaluation
V2 = T1V1T2
V2 = 293.151×10−3×323.15 = 1.1 x 10−3 m3
Worked example - Applying Charles' law in a balloon
A helium-filled balloon has a volume of 1 x 10-3 m3 at 20°C.
Calculate the volume of the helium when the temperature is increased to 50°C.
Step 1: Charles' law formula
T1V1=T2V2
Step 2: Convert celsius to kelvin
to convert form °C to K, add 273.15
20°C = 293.15 K
50°C = 323.15 K
Step 3: Rearrangement
V2 = T1V1T2
Step 4: Substitution and correct evaluation
V2 = 293.151×10−3×323.15 = 1.1 x 10−3 m3