Energy In Simple Harmonic Motion
This lesson covers:
- Understanding the role of the restoring force and the various types of potential energy
- Examining the energy exchange between potential and kinetic energy throughout a complete cycle
- Observing the changes in potential and kinetic energy during different phases of motion
- Explaining the concept of mechanical energy and its conservation in oscillatory systems
- A practical example to calculate mechanical energy in a specific scenario
The restoring force and types of potential energy
In any type of oscillatory motion, such as a swinging pendulum or a vibrating spring, there exists a crucial force known as the 'restoring force'. This force consistently acts to return the oscillating object back to its central equilibrium position.
The specific type of potential energy present in the system is determined by the nature of the restoring force:
- Gravitational Potential Energy is involved when dealing with a pendulum. This is due to gravity pulling the pendulum towards its lowest point.
- Elastic Potential Energy comes into play for a mass attached to a spring, where the spring's force tries to restore it to the resting position.
Exchange between potential and kinetic energy
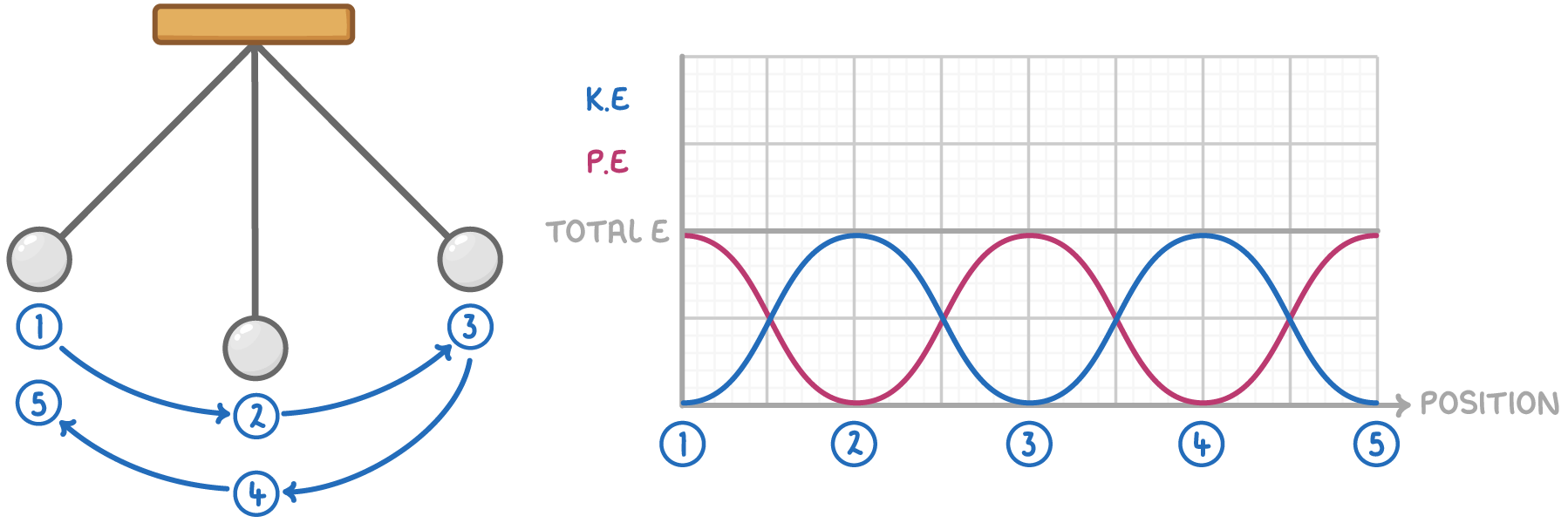
During one full oscillation cycle, energy within the system is continuously transformed between potential and kinetic forms, guided by the restoring force:
- When the object moves closer to the midpoint, its potential energy is converted into kinetic energy.
- As the object moves away from the midpoint, this kinetic energy is then transformed back into potential energy.
Key points:
- At the points of maximum displacement, which are the furthest points from equilibrium, the potential energy is at its peak, while kinetic energy is momentarily zero.
- Conversely, at the midpoint, which is the equilibrium position, the potential energy is at its lowest (zero), and kinetic energy is at its maximum.
- In an ideal system, where external forces like friction are negligible, this total energy remains constant.
Worked example - Calculating mechanical energy in a mass-spring system
Calculate the mechanical energy of a 2 kg block attached to a spring. The block oscillates with a maximum displacement of 5 cm on either side of the equilibrium position, and the spring constant is 40 N m-1.
Step 1: Formula for Spring Potential Energy
The potential energy in a spring (E) is given by the formula: 21kx2
Step 2: Converting cm to m for Displacement (x)
To convert from cm to m, divide by 100
5 cm = 0.05 m
Step 3: Substitution and Correct Calculation
Now, substitute the values into the formula:
E = 21×40×0.052
E = 21×40×0.0025=0.05 J
Step 4: Determining Mechanical Energy at Maximum Displacement
At the point of maximum displacement, all the energy in the system is potential, with kinetic energy being zero.
Total mechanical energy = Potential energy = 0.05 J