Photons

This lesson covers: 

1. What electromagnetic radiation is
2. How it can be described by frequency and wavelength
3. The idea photons as discrete packets of electromagnetic energy
4. Equations linking photon energy, frequency, wavelength and the Planck constant
5. Photon momentum

The electromagnetic spectrum

Visible light is part of the electromagnetic (EM) spectrum - which includes all possible EM frequencies from radio waves to gamma rays.

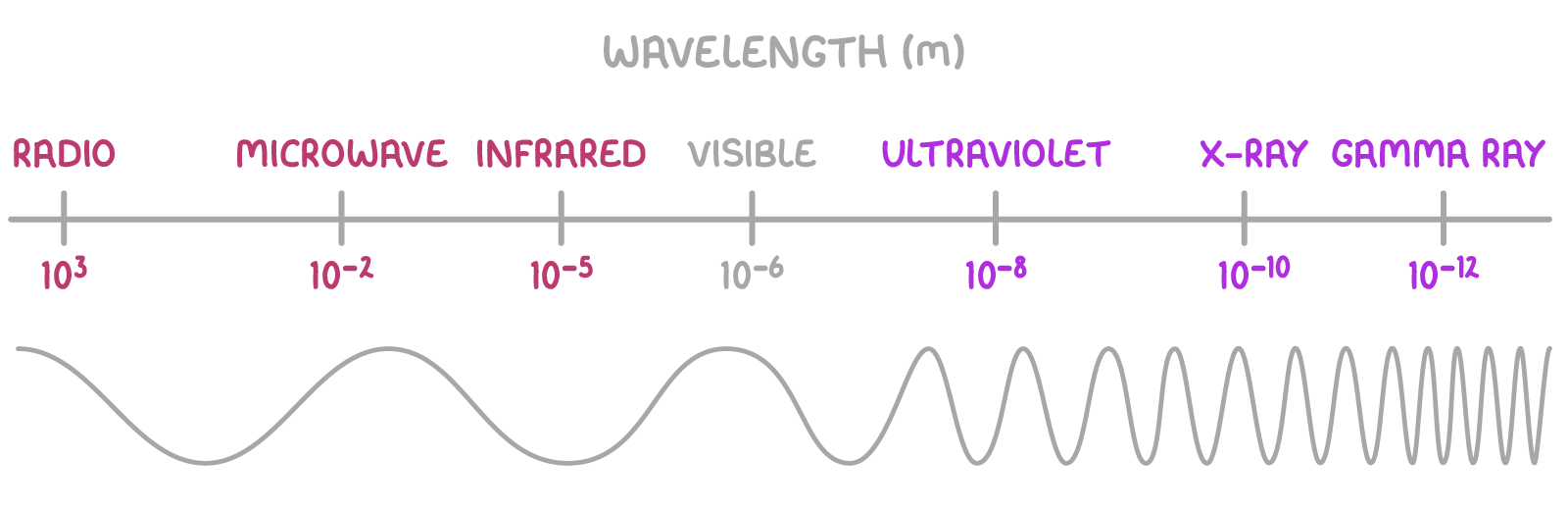
Higher frequency EM radiation carries more energy.

Electromagnetic radiation travels in discrete photons

Electromagnetic radiation propagates in discrete bundles called photons.

Each photon carries a quantum of EM energy related to the frequency by Planck's constant:

E = h f

Where:

E = photon energy in J

h = Planck's constant (6.63 x 10^-34 J s)

f = frequency (Hz)

We also know:

c=fλ

Where:

c = speed of light (3 x 10⁸ m s^-1)

f = frequency (Hz)

λ = wavelength (m)

Combining these gives an equation for photon energy in terms of wavelength:

E = λh c​

Photons are discrete packets of EM radiation with energy proportional to their frequency or inversely proportional to their wavelength.

Worked Example: Calculating photon energy

Calculate the energy of a photon with a frequency of 6 x 10¹⁴ Hz.

Step 1: Formula

E=hf

Step 2: Substitution and correct evaluation

E = 6.63 x 10^-34 x 6 x 10¹⁴ = 3.978 x 10^-19 J

Worked Example 2: Calculating photon wavelength

Calculate the wavelength of a photon which has an energy of 1.02 x 10^-16 J.

Step 1: Formula

E = λh c​

Step 2: Rearrangement

λ=Ehc​

Step 3: Substitution and correct evaluation

λ=1.02×10−166.63×10−34×3×108​=1.95×10−9 m

Photon momentum

Photons have momentum as well as energy. The momentum (p) of a photon is given by:

p =cE​

Where:

p = momentum (kg m s^-1)

E = energy (J)

c = speed of light in (3 x 10⁸ m s^-1)

We can substitute the photon energy equation into this:

p = chf​ = λh​

So photon momentum is directly proportional to frequency and inversely proportional to wavelength.