Specific Heat Capacity

This lesson covers: 

1. Defining specific heat capacity
2. The equation linking energy, mass, specific heat capacity, and temperature change
3. Methods to experimentally determine specific heat capacity
4. Using the method of mixtures to estimate specific heat capacity

Specific heat capacity

Specific heat capacity (c) is the amount of energy required to raise the temperature of 1 kg of a substance by 1 K or 1°C.

Substances with a higher specific heat capacity need more energy to increase their temperature.

The relationship between energy change, mass, specific heat capacity, and temperature change is given by:

E = m c Δθ

Where:

• E = Energy change (J)
• m = Mass (kg)
• c = Specific heat capacity (J kg^-1°C^-1)
• Δθ = Change in temperature (K or °C)

Worked example - Calculating specific heat capacity

0.250 kg of water is heated from 12.1°C to 22.9°C using a 12 V, 5.30 A heater over 205 s. Calculate the specific heat capacity of water.

Step 1: Calculate heat energy supplied

E = V I t = 12 x 5.30 x 205 = 13,038 J

Step 2: Calculate temperature change

Δθ = 22.9 - 12.1 = 10.8 °C

Step 3: Rearranged specific heat capacity formula

c = mΔθE​

Step 4: Substitution and correct evaluation

c=mΔθE​=0.250×10.813,038​=4,828.9 J kg−1K−1

Determining specific heat capacity experimentally

To find the specific heat capacity of a substance, you need to heat it and measure:

• The energy supplied
• The mass
• The resulting temperature change

Then use these values in the equation above to calculate c.

For a solid:

For a liquid:

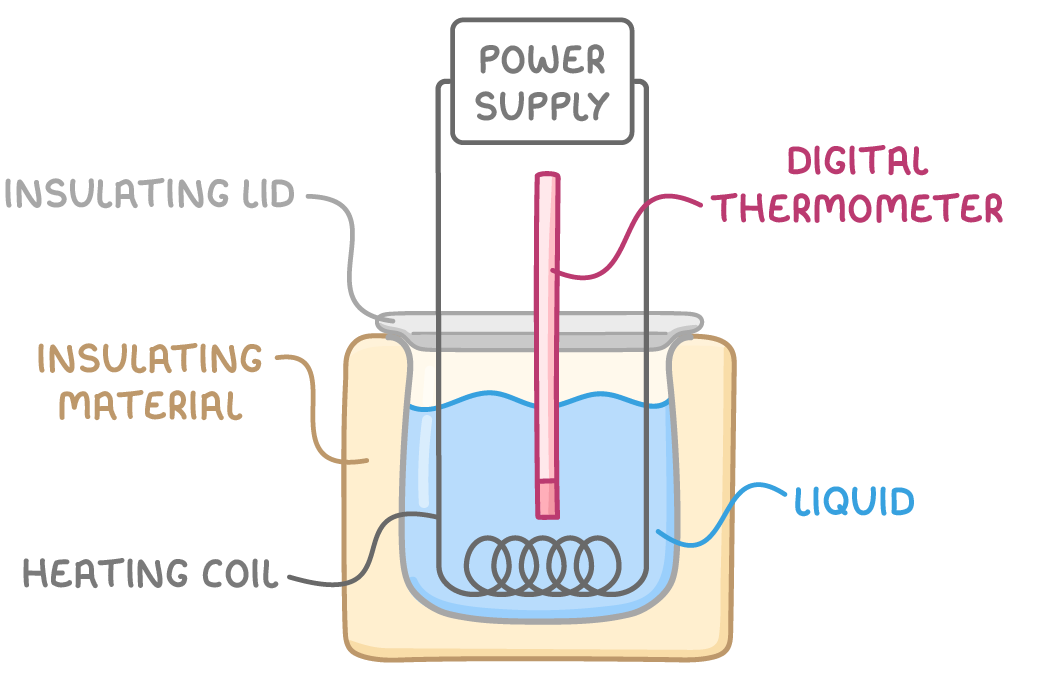
Method:

1. Heat the substance, aiming for a temperature rise of about 10 K.
2. Calculate the heating energy (E) using E=VIt.
3. Measure the mass (m) and temperature change (Δθ).
4. Substitute into E=mcΔθ to calculate c.

Estimating specific heat capacity using the method of mixtures

This method estimates a metal's specific heat capacity:

Steps:

1. Heat a metal block of mass mc​ to T1​.
2. Transfer it into a calorimeter containing water of mass mw​ at T0​.
3. Measure the final steady temperature T.
4. Heat gained by water = heat lost by metal block mc​c(T−T0​)=mw​c(T1​−T)
5. Rearrange to find c: c=mc​(T−T0​)mw​c(T1​−T)​

Worked Example - Calculating specific heat capacity using method of mixtures

A metal block of mass 0.5 kg is heated to 100°C and then placed in a calorimeter containing 0.4 kg of water at 20°C. The final temperature of the mixture is 25°C. Calculate the specific heat capacity of the metal, assuming the specific heat capacity of water is 4,200 J kg^-1 K^-1.

Step 1: Formula for heat transfer

Heat lost by metal = Heat gained by water

mc​cc​(T1​−T)=mw​cw​(T−T0​)

Where:

• m_c = mass of the metal block (kg)
• c_c = specific heat capacity of the metal (J kg^-1 K^-1)
• T₁ = initial temperature of the metal (°C)
• T = final temperature of the mixture (°C)
• m_w = mass of the water (kg)
• c_w = specific heat capacity of water (J kg^-1 K^-1)
• T₀ = initial temperature of the water (°C)

Step 2: Rearrange to find the specific heat capacity of the metal

cc​=mc​(T1​−T)mw​cw​(T−T0​)​

Step 3: Substitution and correct evaluation

cc​=0.5×(100−25)0.4×4200×(25−20)​=0.5×758400×5​=37.542000​=1120 J kg−1K−1

Worked Example - Estimating Energy Required to Heat a Substance

Calculate the energy required to heat 0.75 kg of aluminium from 15°C to 75°C. The specific heat capacity of aluminium is 900 J kg^-1 K^-1.

Step 1: Specific heat capacity formula

E=mcΔθ

Step 2: Calculate temperature change

Δθ=75−15=60∘C

Step 3: Substitution and correct evaluation

E=0.75×900×60=40,500 J

Worked example - Determining final temperature in a calorimetry experiment

0.3 kg of iron at 150°C is placed in 0.2 kg of water at 25°C in a calorimeter. The specific heat capacity of iron is 450 J/kg·K, and that of water is 4,200 J/kg·K. Calculate the final temperature of the mixture.

Step 1: Formula for heat transfer in a calorimetry experiment

Heat lost by iron = Heat gained by water

m_ironc_iron(T_{initial(iron)} - T) = m_waterc_water(T - T_{initial water})

Step 2: Rearrange to find final temperature (T_final)

0.3×450×(150−T)=0.2×4200×(T−25)

Step 3: Substitution and correct evaluation

135×(150−T)=840×(T−25)

20250−135T=840T−21000

975T=41250

T=97541250​≈42.3∘C