Wave-Particle Duality
This lesson covers:
- How light can demonstrate both wave and particle properties
- Explanation of the photoelectric effect and how it supports the particle model of light
- De Broglie's hypothesis proposing the wave nature of matter
- Confirmation of electron wave properties through electron diffraction experiments
- Calculating de Broglie wavelengths and relating wavelength to momentum
- Why macroscopic particles do not exhibit wave properties
- The process of scientific validation through experimentation
Wave and particle models of light
Historically, light was modelled as either a wave or a particle, but modern quantum physics recognises light can demonstrate both wave and particle characteristics.
| Properties | Evidence |
|---|---|
| Wave properties | interference and diffraction patterns |
| particle properties | photoelectric effect |
De Broglie's hypothesis of matter waves
In 1924, Louis de Broglie proposed that just as light exhibits both wave and particle properties, particles should also demonstrate wavelike behaviour.
He related the wavelength (λ) to the momentum (p) of a particle:
λ=ph
Where:
- λ = Wavelength (m)
- h = Planck's constant (J s)
- p = momentum (kg m s-1)
This is known as the de Broglie wavelength.
Initially met with skepticism, de Broglie's revolutionary idea was soon confirmed experimentally.
Confirming the wave properties of electrons
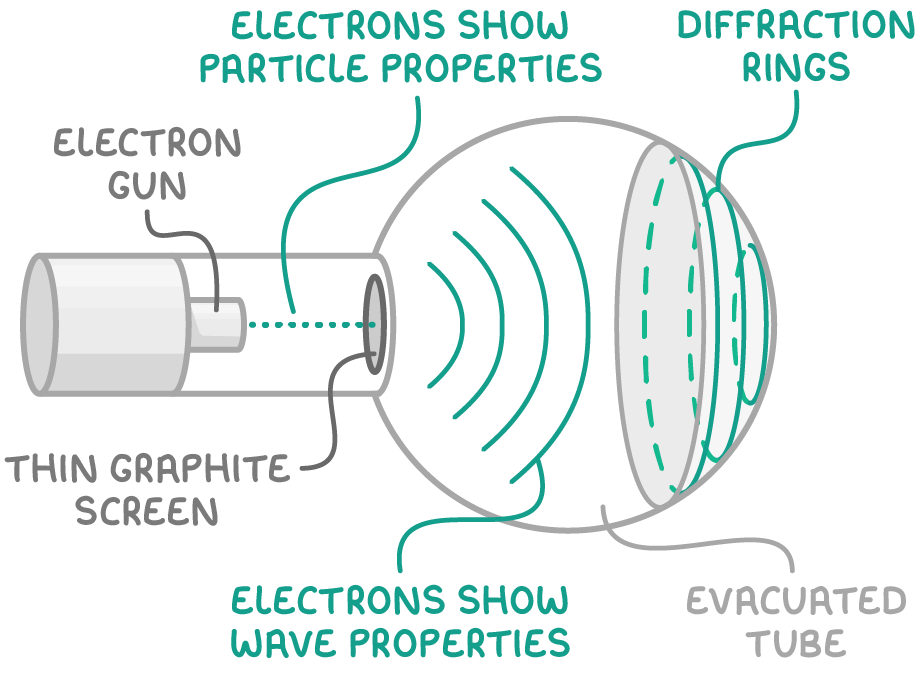
Electron diffraction experiments demonstrate the wave properties of electrons by showing diffraction patterns when electrons interact with crystals.
Key observations:
- Electron diffraction patterns have similar spacings to X-ray diffraction patterns
- Faster electrons diffract less than slower electrons
This evidence supports electron waves which have:
- Shorter wavelengths for faster moving electrons
- Longer wavelengths for slower electrons
These observations align with de Broglie's relationship between wavelength and momentum.
Relating de Broglie wavelength to momentum
The de Broglie equation can be rearranged to determine an electron's wavelength:
λ=mvh
Where:
- λ = Wavelength (m)
- h = Planck's constant (J s)
- m = Particle mass (kg)
- v = Particle speed (m s-1)
Worked example - calculating an electron's de Broglie wavelength
An electron with mass 9.11×10−31 kg moves at 7×106 m/s. Determine its de Broglie wavelength.
Step 1: Formula
λ=m vh
Step 2: Substitution and correct evaluation
λ=(9.11×10−31)(7×106)6.63×10−34=1.04×10−10 m
Limits on observing quantum effects
Macroscopic particles do not demonstrate measurable wave effects because their de Broglie wavelengths are extremely small.
For diffraction to occur, the particle must interact with an object around the same size as its wavelength.
Eg. A 0.058 kg ball moving at 100 m/s has a wavelength of 1.14×10−34 m, much smaller than atomic nuclei.