The Photoelectric Effect

This lesson covers: 

1. The key observations of the photoelectric effect
2. How the photoelectric effect provides evidence for light's particle nature
3. The photoelectric threshold frequency and work function
4. How Einstein explained the photoelectric effect using photons
5. The quantification of maximum photoelectron kinetic energy

The photoelectric effect

The photoelectric effect is when light above a particular frequency is incident on a metal surface, causing electrons to be emitted from the surface.

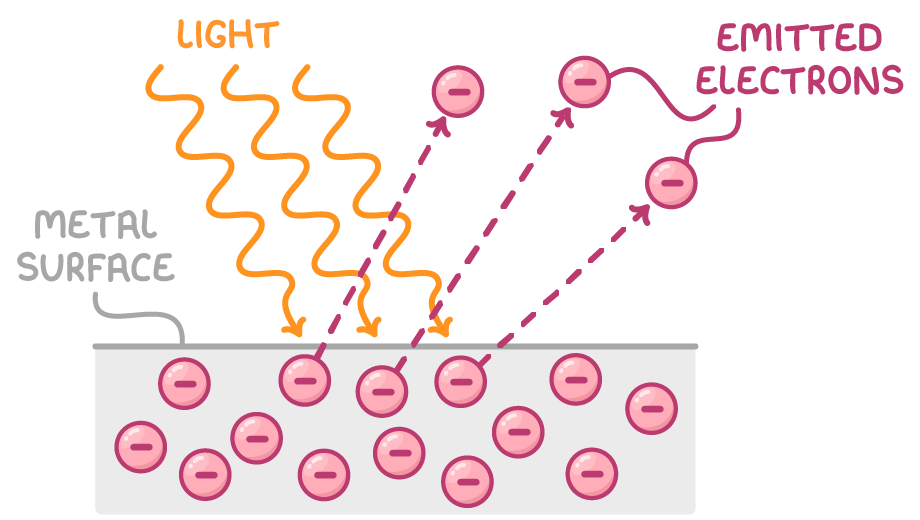
Key observations:

• Photoelectrons are only emitted if the incident light is above a particular frequency known as the threshold frequency.
• The maximum kinetic energy of the emitted photoelectrons does not change when the incident light intensity is increased.
• As light intensity is increased, the number of photoelectrons emitted increases.
• Increasing the frequency of incident light, increases the maximum kinetic energy of the photoelectrons emitted.
• There is a one-to-one interaction between photons and electrons. This means one photon can cause the emission of one photoelectron. 

These observations contradict the wave theory of light and provides evidence for the particle nature of light.

Photons explain photoelectric effect

The photon theory proposes light propagates in discrete quanta or particles called photons.

Each photon has energy proportional to light frequency. Einstein used this concept to explain photoelectric observations.

The energy of a photon is related to the photon frequency by:

E = h f 

Where:

E = photon energy (J)

h = planck’s constant = 6.63 x 10^-34 J s

f = photon frequency (Hz)

Threshold frequency and work function

If the frequency of the incident light is too low, photoelectrons will not be emitted from the metal surface.

The lowest frequency of light that causes electrons to be emitted is known as the threshold frequency.

This links to the work function (ϕ) - the minimum photon energy needed to release an electron from the surface of the metal.

The threshold frequency equation is:

fo​=hϕ​

Where:

f_o = threshold frequency (Hz)

ϕ = work function (J)

h = Planck constant (6.63 x 10^-34 J s)

Calculating maximum photoelectron energy

Einstein derived an equation for the maximum kinetic energy (Emax​) of emitted photoelectrons:

Emax​= h f −ϕ

This can also be expressed in terms of the electron mass (m) and velocity (vmax​):

21​mvmax2​=hf−ϕ

This equation allows photoelectric effect calculations using photon properties, cementing the particle model of light.

Worked example: Calculating the kinetic energy of a photoelectron.

Calculate the maximum kinetic energy of photoelectrons emitted from a metal surface with a work function of 2.3 eV, when light of frequency 1.4 x 1016 Hz is incident on the metal surface.

Step 1: Formula

Emax​= h f − ϕ

Step 2: Convert eV into J

to convert from eV into J, multiply by 1.6 x 10−19

2.3 eV = 3.68 x 10−19 J

Step 3: Substitution and correct evaluation

Emax​ = h f − ϕ

Emax​=(6.63×10−34×1.4×1016)−3.68×10−19=8.91×10−18 J

Stopping potential

The maximum kinetic energy (E_max) of emitted photoelectrons can be measured using stopping potential.

Photoelectrons can be made to lose energy by going against a potential difference (V). The potential that stops the fastest electrons is the stopping potential (V_s).

The key equation linking work done on electrons to their maximum kinetic energy is:

eV_s = E_kmax

Where:

e = electron charge (1.6 x 10−19 C)

V_s = stopping potential (V)

E_kmax = maximum kinetic energy (J)