Faraday's Law

This lesson covers: 

  1. How relative motion between a conductor and magnetic field causes an e.m.f. to be induced.
  2. Understanding Faraday's law relating induced e.m.f., rate of flux change, and flux linkage.
  3. Determining flux linkage in coils and rods from magnetic flux density and area.
  4. Calculating induced e.m.f. using Faraday's law given data on flux change over time.
  5. Working through calculations relating induced e.m.f., flux linkage change, and time.

Electromotive force induced in moving conductors

When a conductor, such as a rod, moves through a magnetic field, the electrons inside the conductor are forced to one end due to the magnetic force. This movement creates a separation of charge, which induces an electromotive force (e.m.f.) across the conductor, akin to connecting a battery.

This induced e.m.f. enables a current to flow if the conductor is part of a complete circuit.

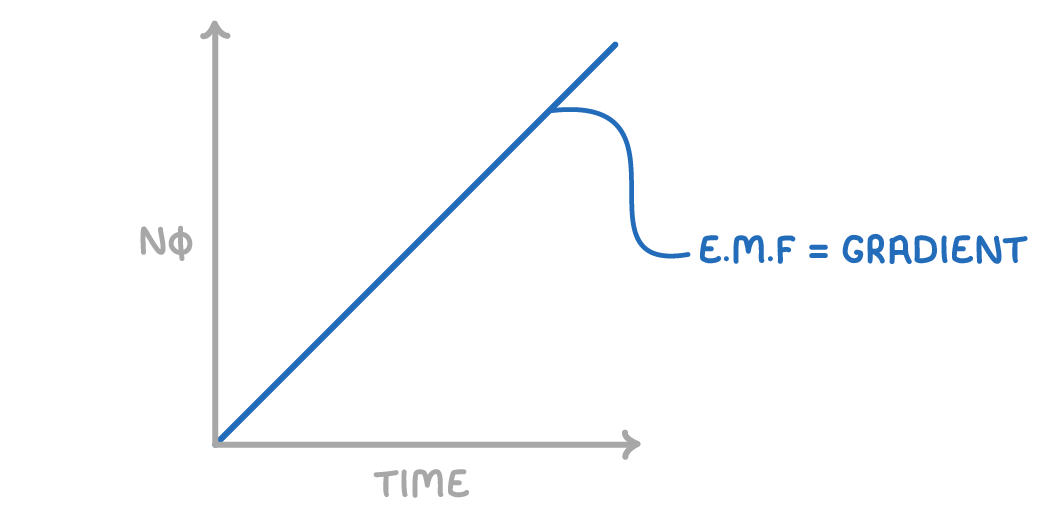
Faraday's law - induced e.m.f. proportional to rate of flux change

Michael Faraday discovered that the magnitude of the induced e.m.f. is directly proportional to the rate of change of flux linkage.

This principle is encapsulated in Faraday's law:


ϵ=−ΔtNΔϕ​


Where:

  • ε = induced e.m.f. (V)
  • N = number of turns in a coil
  • φ = magnetic flux (Wb)
  • t = time (s)


This law implies that a greater change in flux over a given time, or more turns in the coil, will result in a higher induced e.m.f.

Graph showing the relationship between time and magnetic flux with the induced e.m.f. represented as the gradient.

Determining magnetic flux

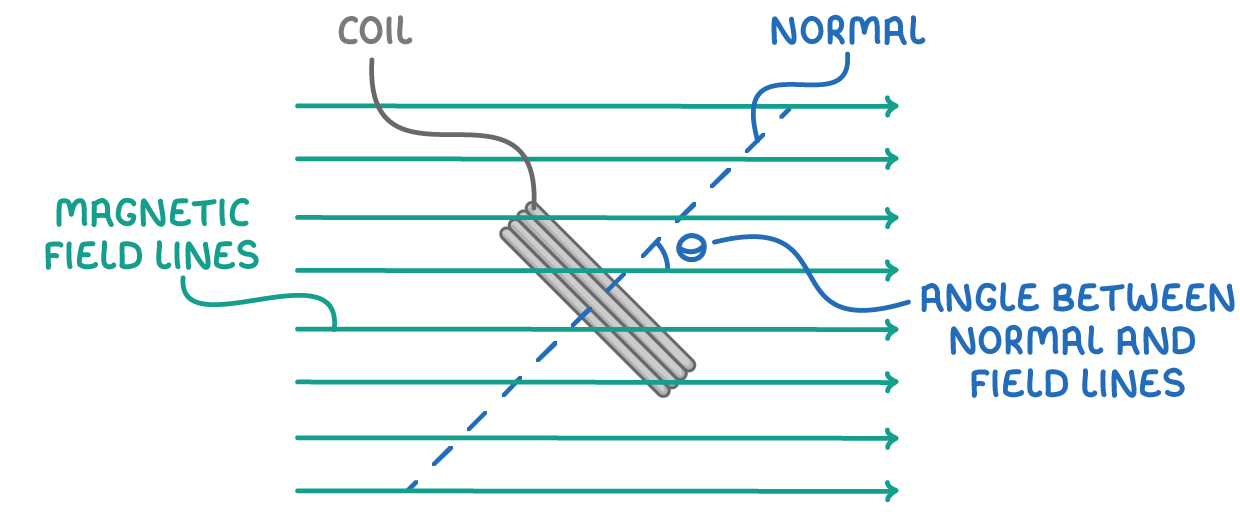
Diagram showing a coil at an angle to magnetic field lines, illustrating the angle between the normal and field lines.

The magnetic flux (φ) through an area (A) perpendicular to the magnetic field (B) is given by:


φ = B A


Where:

  • φ = magnetic flux (Wb)
  • B = magnetic flux density (T)
  • A = area (m2)


When considering multiple turns of a coil, flux linkage becomes relevant:


flux linkage = N φ


For flux at an angle θ to the normal of the area, the equation adjusts to:


flux linkage = B A N cos θ

Calculating induced e.m.f. using Faraday's law

A coil with 100 turns experiences a change in flux from 2 mWb to 0.5 mWb over 0.5 seconds. Calculate the induced e.m.f.


Step 1: Determine change in flux

Initial flux = 2 mWb

Final flux = 0.5 mWb

Flux change = Initial - Final = 2 - 0.5 = 1.5 mWb


Step 2: Formula

ϵ=−ΔtNΔϕ​


Step 3: Substitution and correct evaluation

ϵ=−0.5100×1.5×10−3​=0.3 V

Worked Example - Calculating induced e.m.f. in a rotating coil

A coil with 200 turns is placed in a magnetic field of 0.5 Tesla. The coil's area is 0.1 m2. Initially, the coil is perpendicular to the magnetic field. It is then rotated to a position where its plane is parallel to the magnetic field in 0.2 seconds. Calculate the average induced e.m.f. during this period.


Step 1: Calculate initial and final flux linkage

Initial position (perpendicular):

φ = B A = 0.5 x 0.1 = 0.05 Wb

Final position (parallel):

φ = 0 Wb


Step 2: Calculate change in flux linkage

Δϕ=ϕfinal​−ϕinitial​=0−0.05=−0.05 Wb


Step 3: Formula

ϵ = ΔtN Δϕ​


Step 4: Substitution and correct evaluation

ϵ = 0.2200×0.05​ = 50 V