Refraction At A Plane Surface

This lesson covers: 

  1. Reflection of waves at a boundary or interface
  2. Key concepts in wave refraction
  3. Calculating refractive index using Snell's law
  4. Explaining total internal reflection

Reflection of Waves

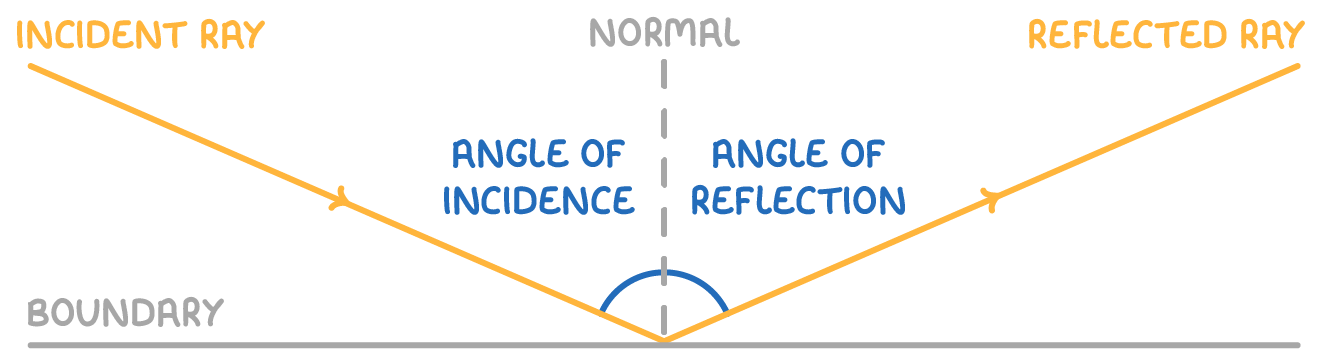
Reflection occurs when a wave hits a boundary between two materials, bouncing off the surface in a new direction. Key properties include:

  • The angle of incidence (i) is the angle at which a wave strikes a surface. It is equal to the angle of reflection (r), which is the angle at which the wave bounces away.


You can observe reflection with:

  • A ripple tank for water waves
  • A ray box for light waves
Diagram showing the reflection of waves with incident ray, reflected ray, angle of incidence, angle of reflection, and normal line.

Refraction: Waves Changing Direction and Speed

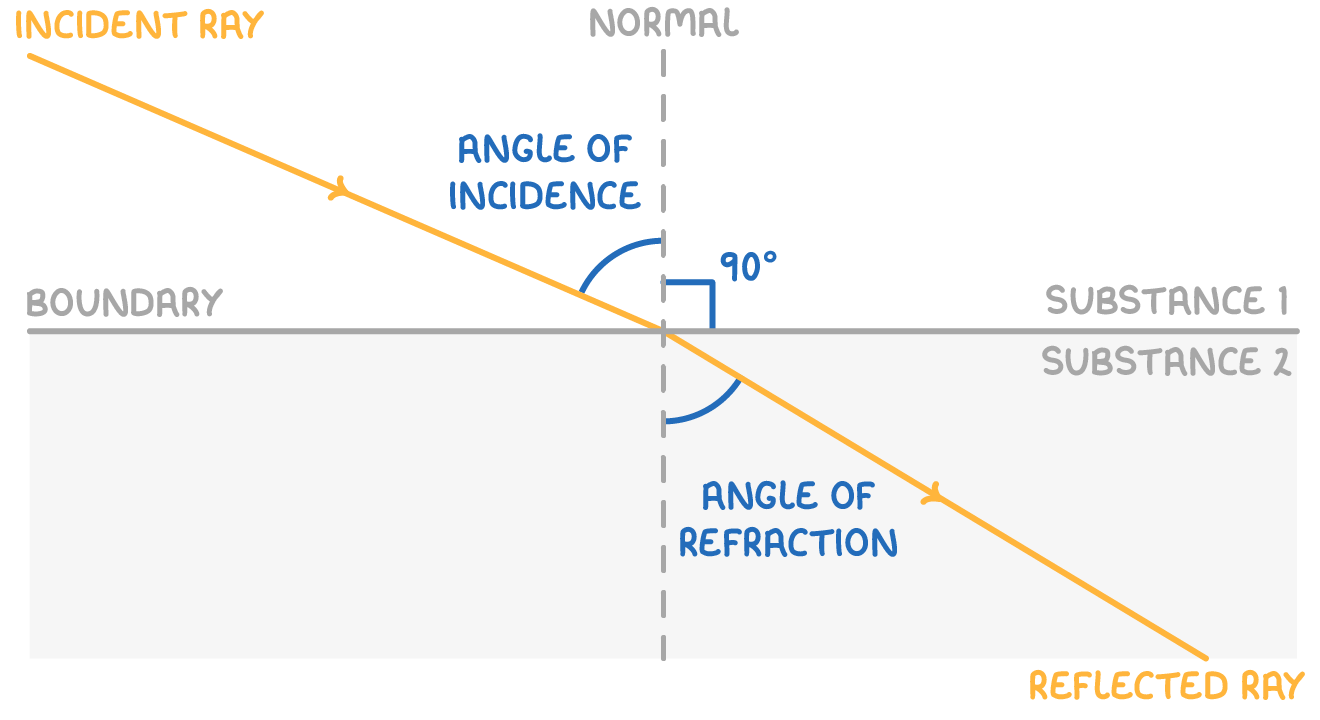
Refraction happens when waves enter a new medium, causing them to change speed and direction.


Important points:

  • If a wave slows down, it refracts towards the normal line; if it speeds up, it refracts away.
  • The change in speed is due to a shift in the wave's wavelength, while its frequency remains constant.
  • Refraction can be seen by passing light through different materials, like glass.
Diagram showing the reflection and refraction of a wave at a boundary between two substances, with angles of incidence and reflection marked.

Using Snell's law to calculate refractive index

The refractive index (n) is the ratio of light's speed in a vacuum (c) to its speed in a material (v):


n = vc​


Snell's law links the angles of incidence and refraction to the refractive indices of two materials:


n2​n1​​=sinθ1​sinθ2​​


Where:

  • θ1​ = Angle of incidence
  • θ2​ = Angle of refraction
  • n1​, n2​ = Refractive indices of each material


By measuring these angles, you can calculate a material's refractive index.

Total internal reflection

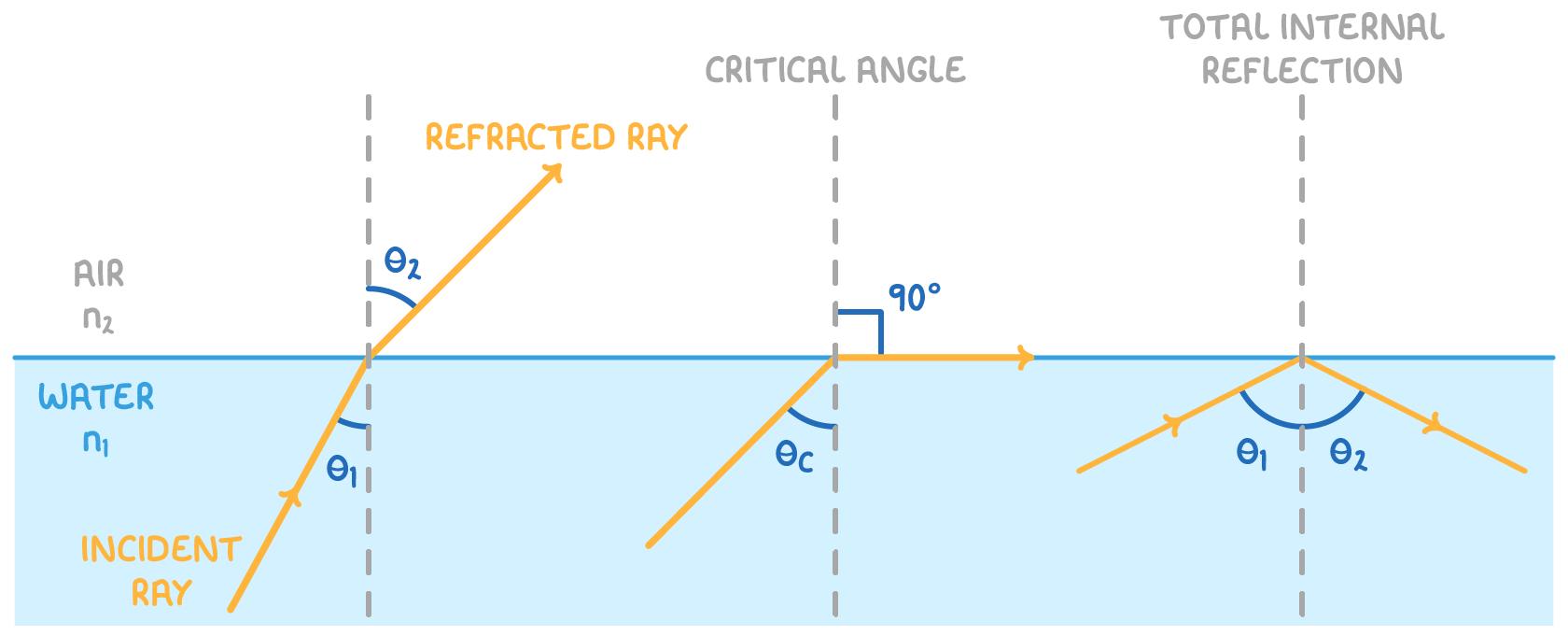
Diagram showing total internal reflection with incident ray, refracted ray, critical angle, and reflected ray.

Total internal reflection occurs when light moves from a denser to a rarer medium (high to low refractive index):

  • It happens at the critical angle (θc), where the angle of refraction is 90°.
  • If the incidence angle (θ) is greater than θc, all light reflects back into the original medium.


The critical angle depends on the refractive index:


sinθc​=n1​


As n increases, θc decreases. Thus, materials with higher refractive indices have lower critical angles for total internal reflection.

Worked example: - Calculating the refractive index using Snell's law

A light ray passes from air into glass, making an angle of 30° with the normal in air. The angle of refraction in the glass is 19°. Calculate the refractive index of the glass.

Step 1: Snell's law formula

n2​n1​​=sinθ1​sinθ2​​

$

Step 2: Rearrangement for (n2)

n2​=n1​×sinθ2​sinθ1​​

Step 3: Substitution and correct evaluation

n2​=1×sin(19)sin(30)​=1.54