Young's Double Slit Experiment

This lesson covers: 

  1. Demonstrating two-source interference with water, sound, and electromagnetic waves.
  2. Young's double-slit experiment to demonstrate interference with light.
  3. Using two microwave transmitters to demonstrate two-source interference.
  4. Calculating wavelengths from interference fringe spacing.

Demonstrating two-source interference

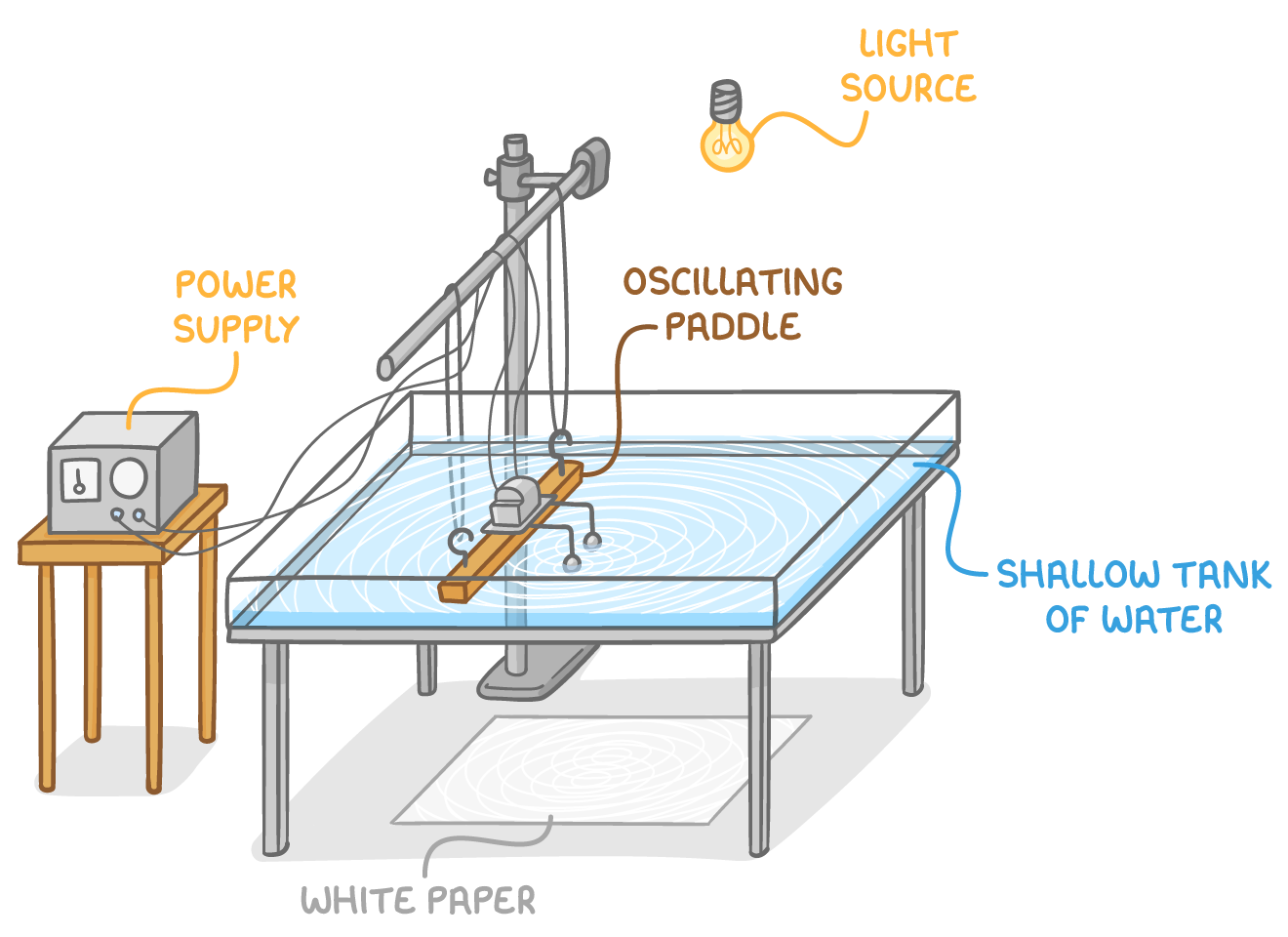
Diagram showing a two-source interference setup with an oscillating paddle in a shallow tank of water, a light source, and white paper.

Two-source interference occurs when waves from two coherent sources combine. We will explore this phenomenon with different types of waves.

Coherent sources have the same frequency and a fixed phase relationship, which is essential for sustained interference.


Water waves:

  • Use two dippers driven by the same oscillator (vibrator) to create waves.
  • This setup ensures the waves from the two dippers are coherent.


Sound waves:

  • Connect two loudspeakers to the same audio oscillator.
  • This setup ensures the sound waves from the loudspeakers are coherent.

Young's double slit experiment

This experiment uses a single laser source to demonstrate two-source interference:

  1. Laser light passes through two narrow slits, causing diffraction.
  2. The slits act as two coherent point sources of light.
  3. An interference pattern of alternating light and dark fringes appears on a screen.
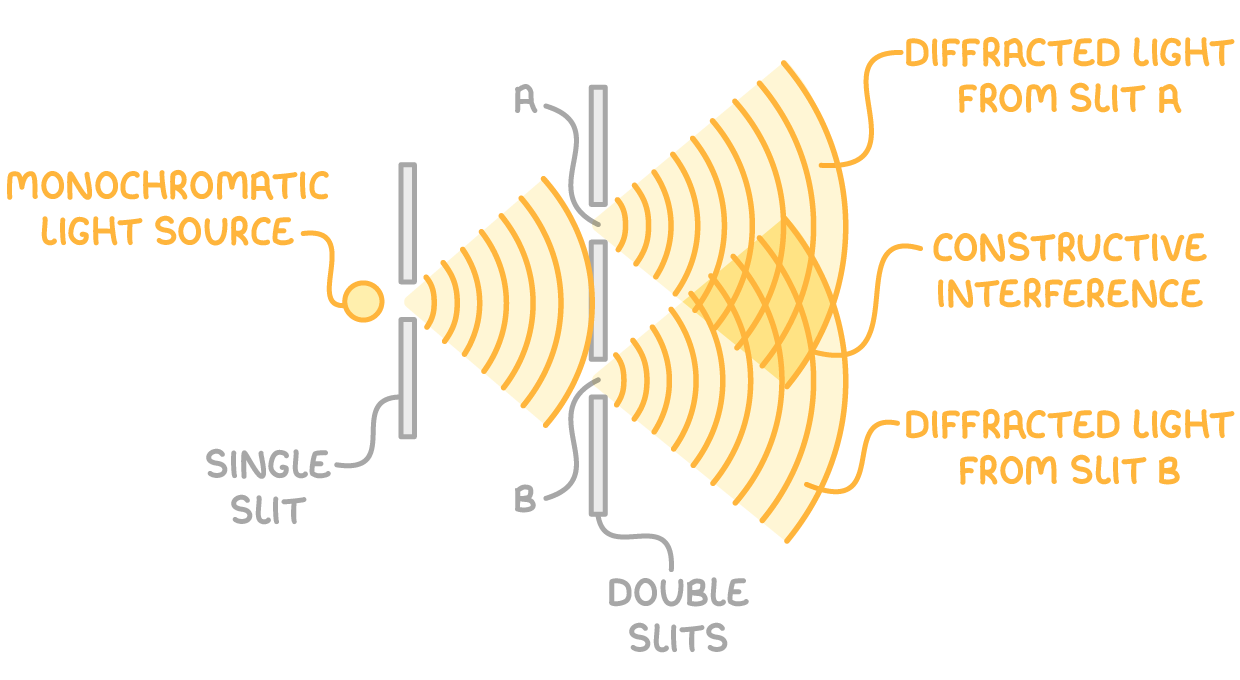
Diagram showing Young's double slit experiment with a single laser source, double slits, and an interference pattern.
  • Maximas (bright fringes) - Observed where the waves from the two slits are in phase and they superpose constructively.
  • Minimas (dark fringes) - Observed where the waves from the two slits are out of phase and they superpose destructively.
Phase differencePath difference
Bright fringe0 or n2π\pi0 or nλ\lambda
Dark fringe(n + 0.5)π\pi(n + 0.5)λ\lambda

Where n = 0,1,2,3,4...

Fringe spacing

The spacing of the fringes is dependent on the wavelength of light, distance between the slits and the screen, and the slit spacing:


w = sλ D​


Where:

  • w = fringe spacing (m)
  • λ = wavelength (m)
  • D = distance from slits to screen (m)
  • s = distance between slits (m)

Worked example - Calculating fringe spacing

Calculate the fringe spacing when a double slit experiment is performed using light of wavelength 650 nm, with the slits placed 1 m away from the screen and the distance between the slits being 0.25 mm.


Step 1: Convert mm to m

To convert from mm to m, divide by 1,000

0.25 mm = 2.5 x 10-4 m


Step 2: Formula

w = sλ D​


Step 3: Substitution and correct evaluation

w = 0.25×10−3650×10−9×1​=0.25×10−6650​=2.6 mm