Alternating Currents

This lesson covers: 

  1. Understanding that alternating currents constantly change direction
  2. Using an oscilloscope to display alternating and direct current waveforms
  3. Calculating root mean square (rms), peak, and peak-to-peak voltages from an oscilloscope trace
  4. Defining rms voltage and current and using them to calculate power
  5. Relating peak, rms, and peak-to-peak voltages for mains electricity

Alternating currents constantly change direction

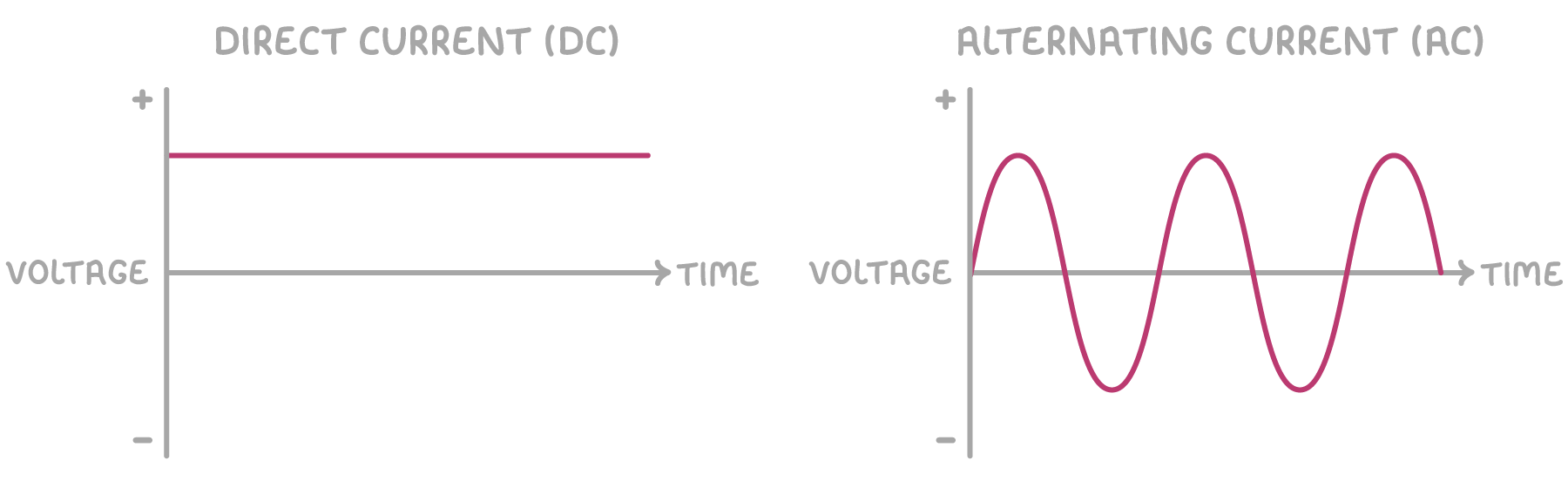
Graph comparing direct current with alternating current, showing voltage over time.

Alternating current (AC) and voltage fluctuate between positive and negative values in a regular pattern. This results in:

  • The current periodically reversing direction.
  • The voltage alternating between positive and negative over time.

Using an oscilloscope to display AC and DC signals

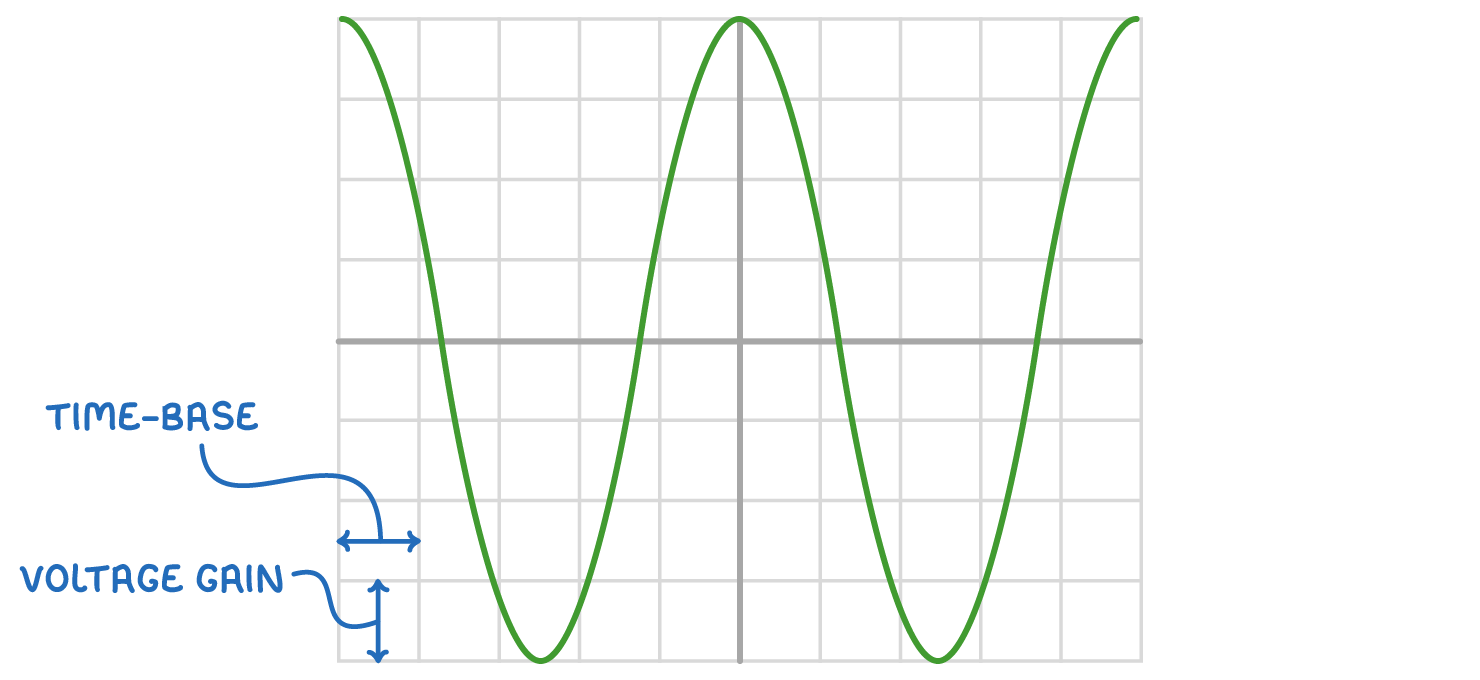
Graph showing an oscilloscope display with AC signal as oscillating lines and DC signal as a straight horizontal line.

An oscilloscope is a tool that visualises electrical signals, representing them as waveforms:

  • AC signals are shown as oscillating lines.
  • DC signals are depicted as straight horizontal lines.


Key oscilloscope settings include:

  • Y-gain - Adjusts the scale for volts per vertical division.
  • Time base -  Controls the speed of the horizontal sweep.

Calculating voltages from an AC oscilloscope trace

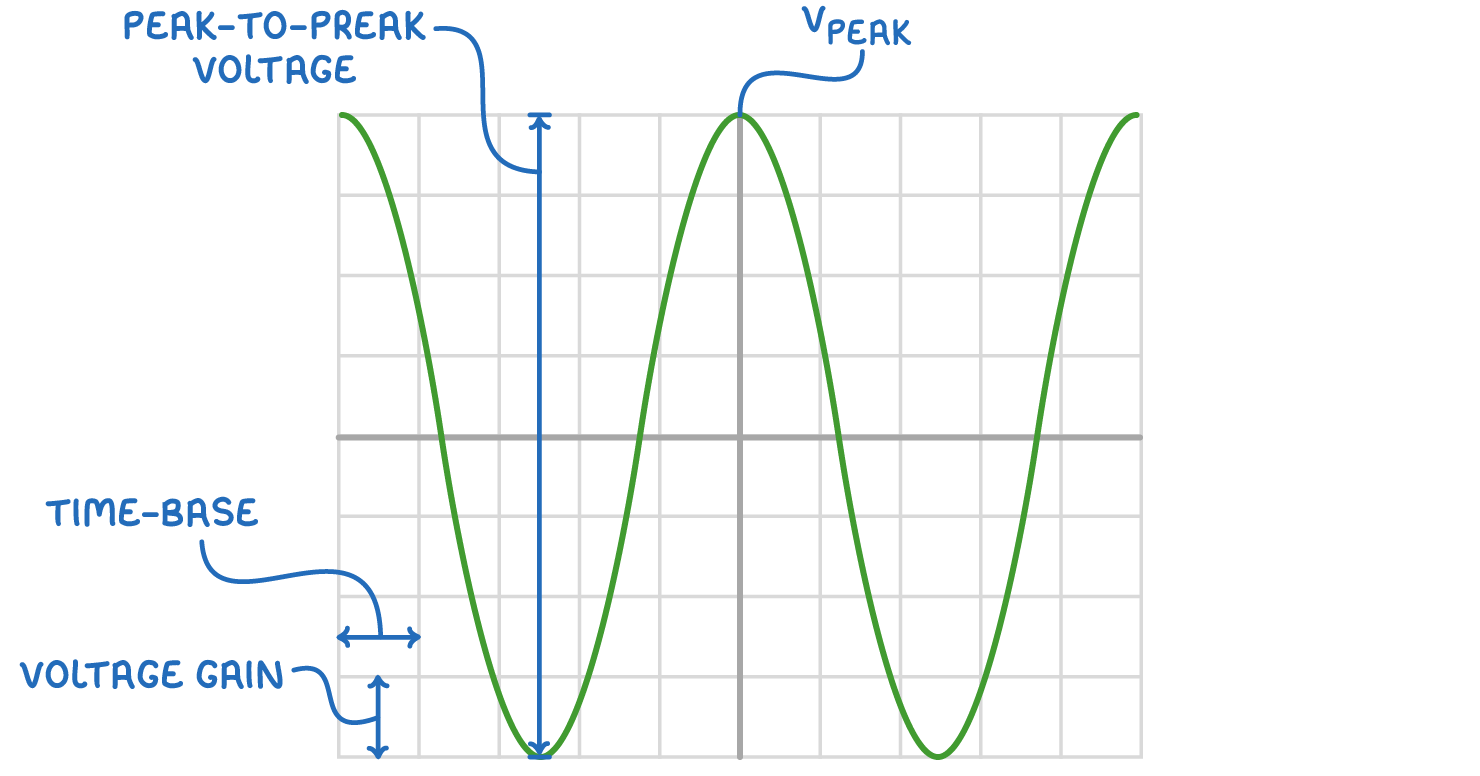
Graph showing an AC oscilloscope trace with peak voltage, peak-to-peak voltage, and time period labelled.

From an oscilloscope trace, you can determine:

  • Peak voltage (V0) - The highest voltage level reached (V).
  • Peak-to-peak voltage - The total voltage change from the peak positive to the peak negative value (V).
  • Time period (T) - The duration of one complete waveform cycle (s).

These readings are essential for understanding signal properties like frequency and power calculations.

Defining RMS voltage and current

For accurate power calculations, root mean square (rms) values are essential:

  • RMS voltage (Vrms) - The equivalent DC voltage that would deliver the same power as the AC signal.
  • RMS current (Irms) - The equivalent DC current for the same power delivery.

For sinusoidal signals:


Vrms​=√2V0​​


Irms​=√2I0​​


Where:

  • Irms = rms current (A)
  • Vrms = rms voltage (V)
  • I0 = peak current (A)
  • V0 = peak voltage (V)


Power calculation formula:

The power of an alternating signal can be calculated using the power formula:


P = Irms x Vrms


Where:

P = power (W)

Irms = rms current (A)

Vrms = rms voltage (V)

Worked example - Calculating RMS voltage of mains electricity

The peak voltage (V0) of the UK mains supply is 325 V. Calculate the rms voltage of the UK mains supply.


Step 1: Formula

Vrms​=√2V0​​


Step 2: Substitution and correct evaluation

Vrms​=√2325​=229.81 V

Relating RMS and peak voltages for mains electricity

The UK mains electricity is characterised by:

  • An RMS voltage of 230 V.
  • A peak voltage (V0) of 325 V.
  • A peak-to-peak voltage of 650 V.
  • A supply frequency of 50 Hz.