Projectile Motion

This lesson covers: 

  1. How to analyse projectile motion by separating horizontal and vertical components
  2. Resolving velocities into horizontal and vertical vectors
  3. Using equations of motion to determine the path and time of flight

Think about horizontal and vertical motion separately

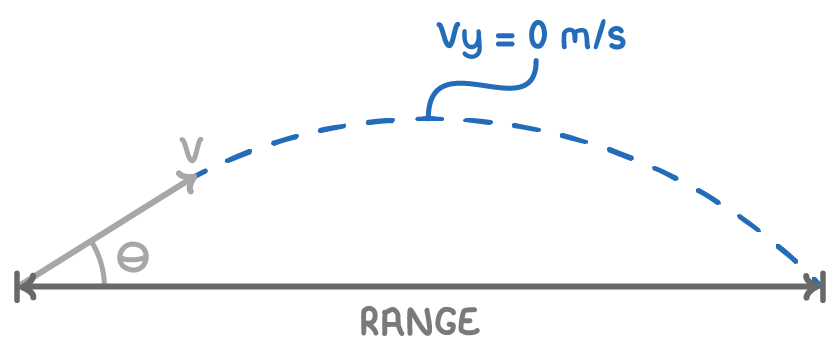
Diagram showing projectile motion with horizontal and vertical components, including initial velocity and highest point where vertical velocity is 0 m/s.
  • A projectile is any object with an initial velocity that then moves freely under gravity
  • The horizontal and vertical components of a projectile's motion are independent
  • The horizontal velocity remains constant while the vertical velocity changes due to gravity
  • This causes the curved path typical of projectile motion
  • The vertical component of velocity is 0 m/s at the highest point

Worked example: Calculating the range of a projectile

Sharon fires a scale model horizontally from 15 m high with a speed of 100 m/s. Determine the time of flight and horizontal distance traveled, assuming no air resistance.

Step 1: Formula

s = u t + 21​a t2


Step 2: Rearrangement

t = √a2 s​​


Step 3: Substitution and correct evaluation

s = 15 m

u = 0 m s−1

v =

a = 9.81 m s−2

t = ?

t = √9.812×15​​

t = 1.7487 s


Step 4: Calculate range

range = horizontal velocity x flight time

range = 100 x 1.7487 = 174.9 m

Motion at an Angle Requires Vector Resolving

  • Forces and velocities can act in any direction
  • Motion must be resolved into horizontal and vertical vectors using trigonometry
  • The initial velocity determines the time of flight and maximum height


Consider an object moving with velocity R at an angle of θ to the horizontal.

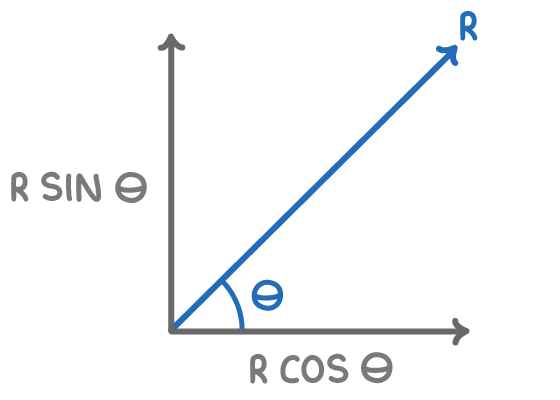
Diagram showing motion at an angle with horizontal component R cos theta and vertical component R sin theta.

The horizontal and vertical components can be calculated:

  • horizontal component = Rcos(θ)
  • vertical component = Rsin(θ)

Worked example: Javelin throw

A javelin is thrown at a speed of 21 m/s at an angle of 45° to the horizontal. Determine the range of the javelin.


Step 1: Calculate vertical and horizontal components

ux​=cos(45°)×21=14.849 m s−1

uy​=sin(45°)×21=14.849 m s−1


Step 2: Calculate time to reach highest point

s = 0 m

uy = 14.849 m s−1

vy = 0 m s−1

a = - 9.81 m s−2

t = ?


t=av−u​

t=−9.810−14.85​=1.5136 s


Step 3: Calculate total flight time

total flight time = 2 x 1.5136 = 3.027 s


Step 4: Calculate range of javelin

range = horizontal velocity x flight time

range = 14.849 x 3.027 = 44.95 m