Energy Levels & Photon Emission

This lesson covers: 

  1. How electrons occupy discrete quantised energy levels in atoms
  2. Electron transitions between energy levels involving photon absorption or emission
  3. Calculating energy differences in electron transitions
  4. Ionisation of atoms when electrons absorb enough energy to escape
  5. An application of electron transitions in fluorescent lighting

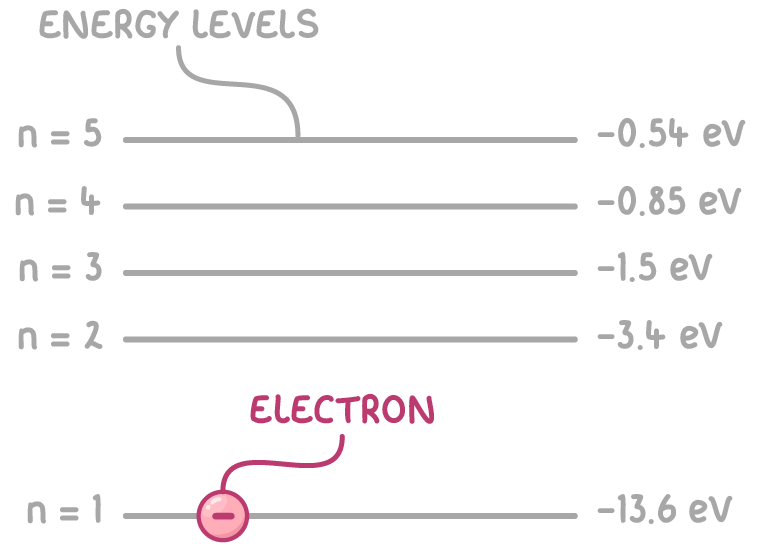
Energy levels in atoms

Instead of orbiting freely, electrons occupy specific discrete energy levels around the nucleus. These levels are given integers:

  • n = 1 is the ground state - the lowest possible energy level
  • Higher n values are higher energy excited states


Since energy levels are quantised, electrons can only occupy or jump between fixed allowed states.

Diagram showing energy levels in atoms with an electron in the ground state and energy values for each level.

Photon absorption and emission in transitions

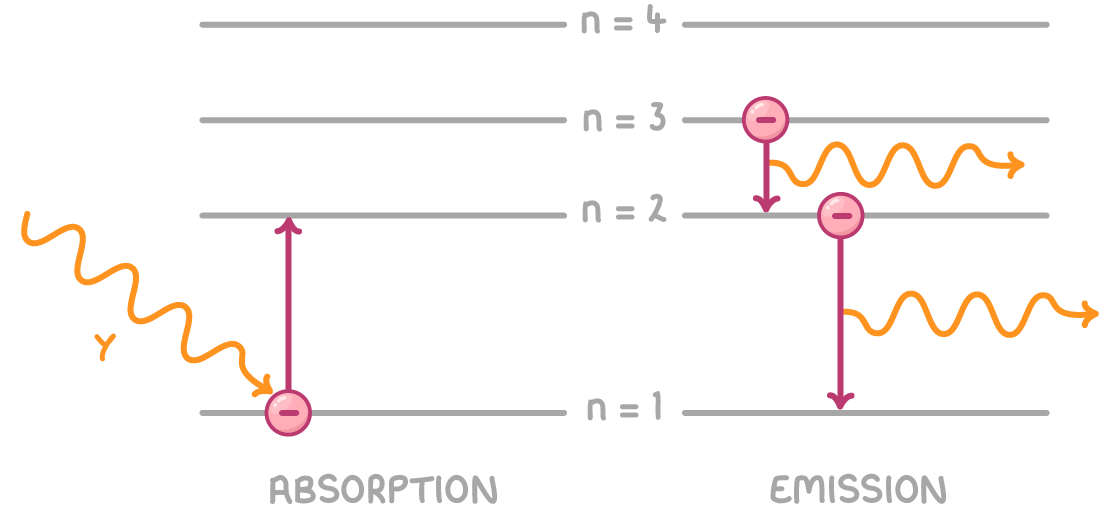
Diagram showing photon absorption and emission with electrons transitioning between energy levels.

Transitions between energy levels involve photons:

  • Absorption - Electrons jump to higher levels by absorbing photon energy
  • Emission - Electrons falling to lower levels and emitting photons


The photon energy equals the difference in energy between levels:


ΔE = Ef​ − Ei​


Where:

ΔE = photon energy (J)

Ef = final energy level (J)

Ei = initial energy level (J)

Worked example: Calculating photon frequency.

Calculate the frequency of a photon which causes an electron to move from the ground state to energy level n=3.

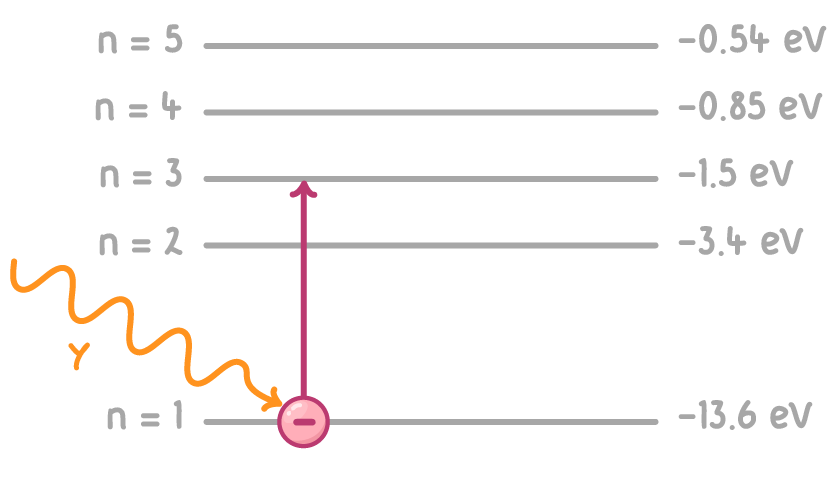
Diagram showing the energy levels of an electron in an atom and the transition from n=1 to n=3 with a photon.

Step 1: Calculate Photon energy

ΔE = Ef​−Ei​

ΔE = −1.5 − −13.6 = 12.1 eV


Step 2: convert eV to J

To convert from eV to J, multiply by 1.6 x 10−19

12.1 eV = 1.936 x 10−18 J


Step 3: Calculate photon frequency

f = hE​

f = 6.63 x 10−341.936 x 10−18​ = 2.92 x 1015 Hz

Ionisation energies

Ionisation removes an electron completely from an atom.

The ionisation energy is the minimum photon energy required to remove an atom from its ground state.

Worked example: Calculating ionisation energy.

Calculate the photon frequency needed to remove an electron from the ground state (-13.6 eV).


Step 1: calculate energy required to remove the electron.

ΔE = Ef​−Ei​

ΔE = 0−−13.6 = 13.6 eV


Step 2: Convert eV to J

to convert from eV to J, multiply by 1.6 x 10−19

13.6 eV = 2.176 x 10−18 J


Step 3: Calculate photon frequency

f = hE​

f = 6.63×10−342.176×10−18​ = 3.28 x 1015 Hz

Fluorescent tubes

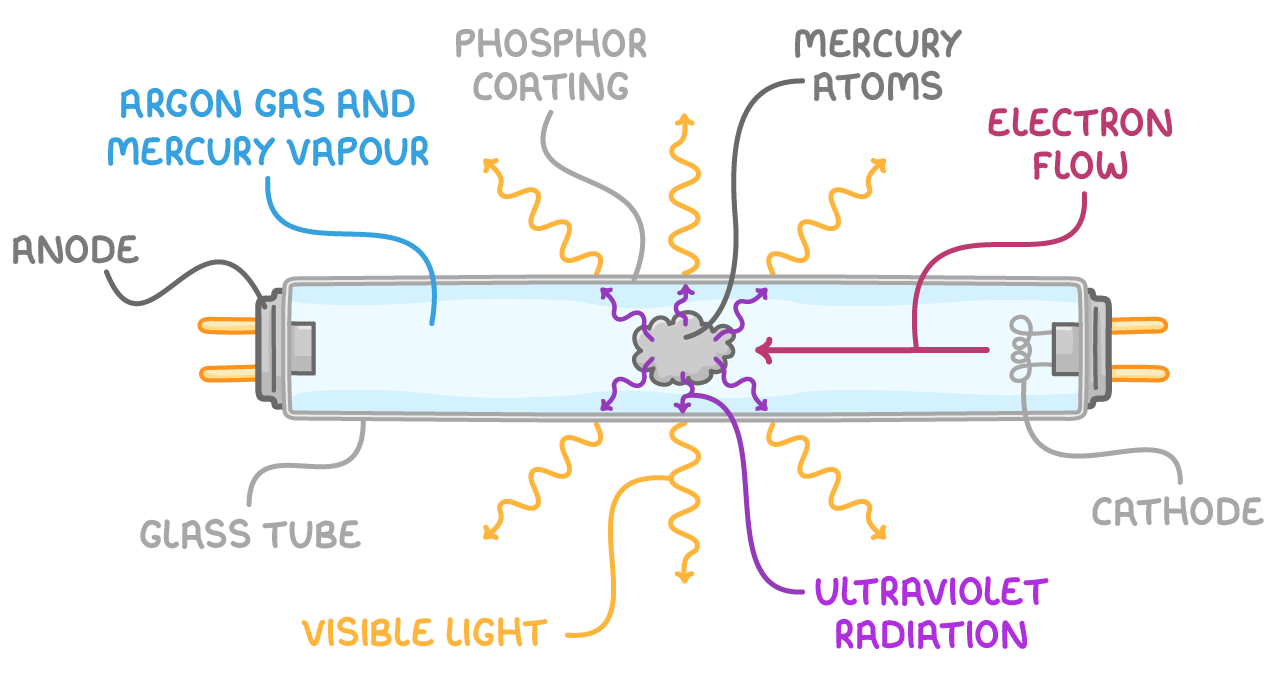
Diagram showing the components and functioning of a fluorescent tube with argon gas, mercury vapour, phosphor coating, electron flow, and visible light emission.

Fluorescent tubes contain mercury vapour which can be excited by accelerated electrons.


How it works:

  1. Electrons are accelerated by an applied voltage across the ends of the tube.
  2. When electrons collide with the mercury vapour, it causes electrons in the vapour to be promoted to a higher energy level.
  3. When these excited electrons fall back to a lower energy level, they emit photons in the UV region of the EM spectrum.
  4. The fluorescent coating of the tube absorbs these UV photons causing electrons in the coating to become excited.
  5. When electrons in the coating de-excite, photons in the visible region are emitted.