Scalars & Vectors
This lesson covers:
- Differentiating between scalar and vector quantities
- Adding vectors graphically and mathematically
- Calculating horizontal and vertical components of vectors
- Analysing systems of forces using free-body diagrams
- Determining the conditions for equilibrium
Scalars and Vectors
A vector is a quantity that has both magnitude and direction, while a scalar only has magnitude.
| Scalars | Vectors |
|---|---|
| distance | displacement |
| speed | velocity |
| temperature | acceleration |
| energy | force |
| time | weight |
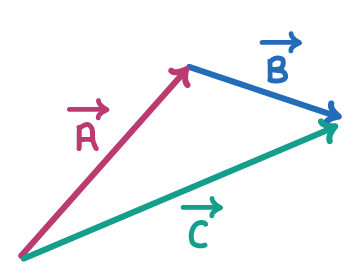
Adding vectors Graphically
To find the resultant vector when adding vectors, we use the tip-to-tail method.
Steps:
- Draw each vector accurately to scale.
- Arrange the vectors tip-to-tail in sequence.
- Measure the resultant vector from the start of the first vector to the tip of the last vector.
Adding perpendicular vectors using trigonometry
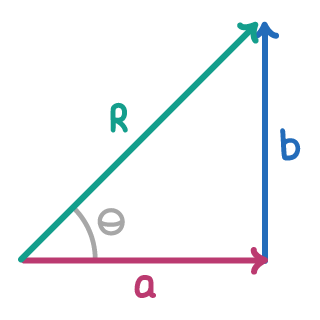
When vectors are perpendicular, we can use trigonometry to find the resultant vector.
Resultant magnitude:
R=√a2+b2
Resultant angle:
θ=tan−1(ab)
Worked Example: Calculating the resultant of two vectors
Vector A has a magnitude of 3 N to the right and vector B has a magnitude of 4 N upwards. Calculate the magnitude and direction of the resultant vector.
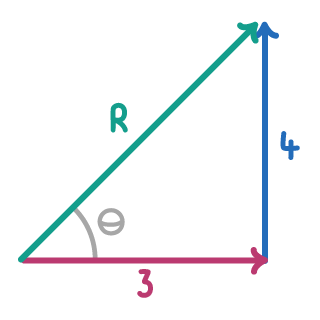
Step 1: Calculate the resultant magnitude
R = √32+42=5 N
Step 2: Calculate the direction of the resultant vector
θ = tan−1(34) = 53.13°
Calculating horizontal and vertical components
Given a resultant vector at an angle, we can calculate its horizontal and vertical components.
Horizontal component (H):
H=Rcos(θ)
Vertical component ():
V=Rsin(θ)
Where is the magnitude of the resultant vector and is the angle with the horizontal.
Worked example: Calculate the horizontal and vertical components of a force
If the magnitude of a force vector is 10 units at an angle of 30° from the horizontal, find its horizontal and vertical components.
Horizontal component: units.
Vertical component: units.
Free-Body Diagrams
Free-body diagrams are used to illustrate all the forces acting on an object.
Key Features:
- The object is isolated from its environment.
- All force vectors are labeled and drawn.
- The relative magnitude and direction of each force are shown.
Equilibrium conditions
An object is in equilibrium when the net force acting on it is zero, resulting in no acceleration.
For two forces, equilibrium is achieved when:
- The forces have equal magnitudes.
- The forces act in opposite directions.
For multiple forces, equilibrium occurs when the sum of all vector forces equals zero.