Moments

This lesson covers: 

  1. Defining moments and how they depend on force and distance from the pivot point
  2. Understanding the principle of moments and equilibrium
  3. Using the principle of moments to analyse levers and joints
  4. Defining a torque produced by a couple (a pair of equal and opposite parallel forces)
  5. Calculating torques in applications like turning handlebars

What is a moment?

A moment, also known as a torque, is the turning effect generated when a force is applied at a distance from a pivot point. The moment's strength (M) is determined by two factors:

  • The magnitude of the force (F)
  • The perpendicular distance (d) from the pivot point

These factors are linked by the formula:

M=F×d


Where:

  • M = Moment (N m)
  • F = Force (N)
  • d = Perpendicular distance from the pivot (m)

Worked example - Calculating the moment of a force

Calculate the moment of a force of 50 N applied at a perpendicular distance of 2 m from a pivot point.

Step 1: Formula

M=F×d


Step 2: Substitution and correct evaluation

M=50×2=100 Nm

Maintaining equilibrium using balanced moments

For an object to remain in equilibrium, the principle of moments states that the total clockwise moments around any point must be equal to the total anticlockwise moments. This can be expressed as:

∑Clockwise Moments=∑Anticlockwise Moments


If the moments are not balanced, the resultant moment will cause the object to rotate.

Moments in levers and joints

Our body's joints function as levers of various classes, allowing our limbs to move efficiently. By applying the principle of moments, we can understand this process better:

Step 1: Identify forces (e.g., muscle force, limb weight) and their distances from the pivot.

Step 2: Calculate the moment each force contributes using (M = F x d).

Step 3: Equate the moments to solve for the unknown force.

Torque produced by a couple

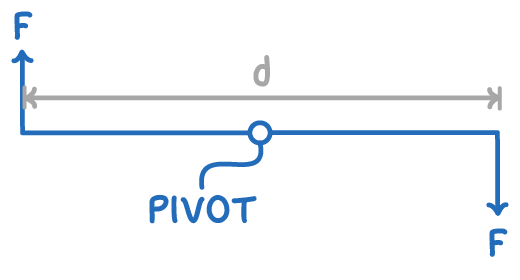
Diagram illustrating the concept of torque produced by a couple with two equal and opposite forces separated by distance d.

A couple consists of two equal and opposite forces acting parallel to each other but separated by a distance. This setup creates a torque, inducing rotation.

The torque (T) calculation is straightforward:


T=F×d


Where:

  • T = Torque (N m)
  • F = Magnitude of one of the forces (N)
  • d = Perpendicular distance between the forces (m)


Couples are pivotal in mechanisms that rotate without moving linearly, such as in

steering vehicles or opening valves.

Worked example: - Calculating torque produced when turning handlebars

A cyclist wishes to sharply turn the handlebars (60 cm in length) by exerting a 20 N force at each end. Let's compute the torque generated.

Step 1: Formula

T = F x d


Step 2: conversion from cm to m

to convert from cm to m, divide by 100

60 cm = 0.6 m


Step 3: substitution and correct evaluation

T = 20 x 0.6 = 12 N m