Radioactive Decay

This lesson covers: 

  1. Defining the half-life (t21​​) of a radioactive isotope
  2. Explaining exponential decay of unstable nuclei over time
  3. Using graphs to determine the half-life from number of undecayed nuclei
  4. Experimental methods to plot count rate decay graphs
  5. Calculating half-life from count rate measurements

Half-Life Definition

The half-life (t21​​) of a radioactive isotope is the time taken for half of the unstable nuclei in a sample to decay. Specifically, it is the time required for the number of undecayed nuclei to reduce to half its original value.


Longer half-lives indicate the isotope remains radioactive for longer periods. Shorter half-lives mean faster decay.

Exponential decay

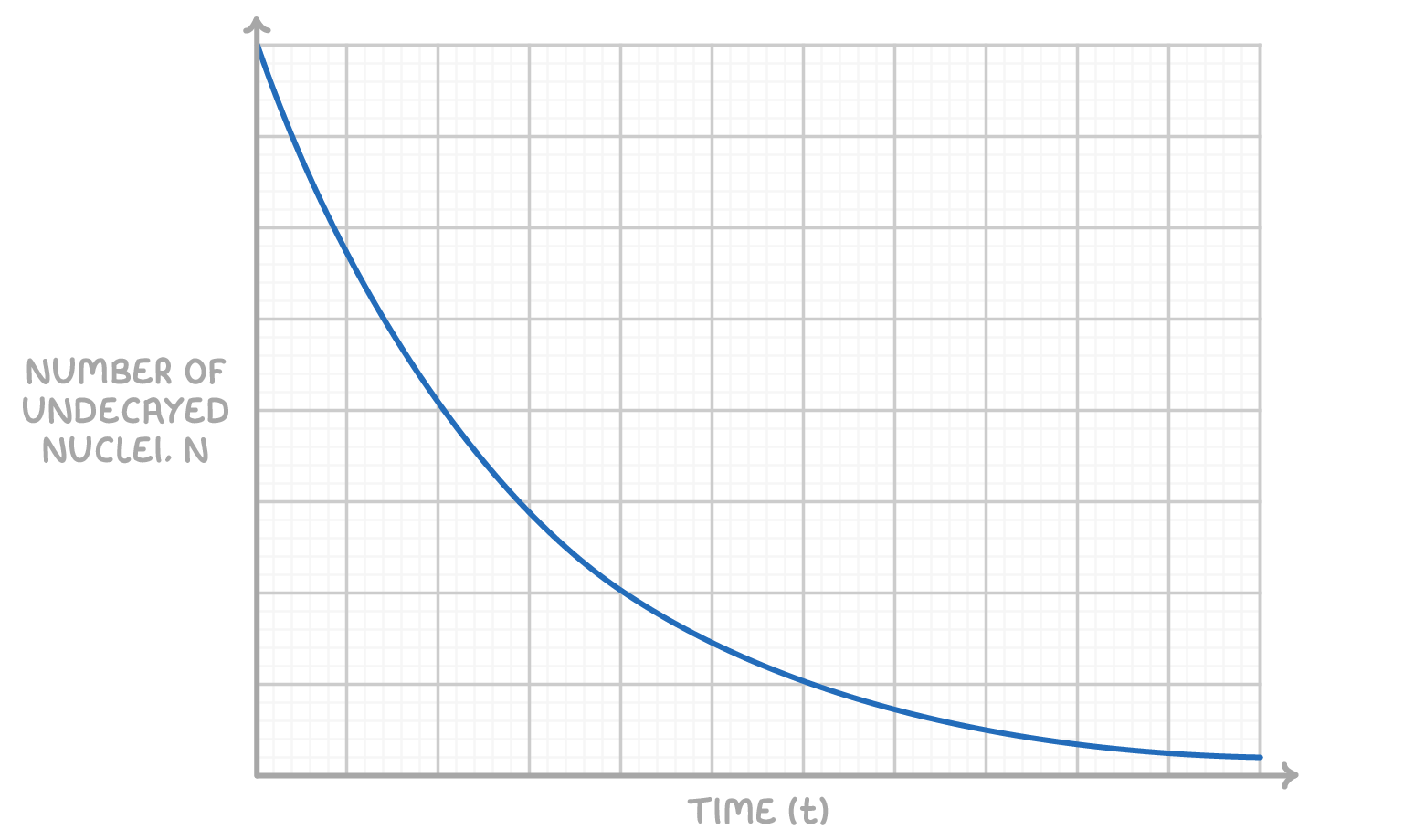
Graph showing the exponential decay of radioactive nuclei over time with number of undecayed nuclei on the y-axis and time on the x-axis.

The decay of radioactive isotopes over time follows an exponential pattern. This makes the exact decay time of individual nuclei unpredictable.

However, the overall rate of decay for a large number of nuclei is predictable using probability statistics. This allows us to plot graphs showing the reduction in the number of undecayed nuclei over time.

Experimentally generating count rate decay graphs

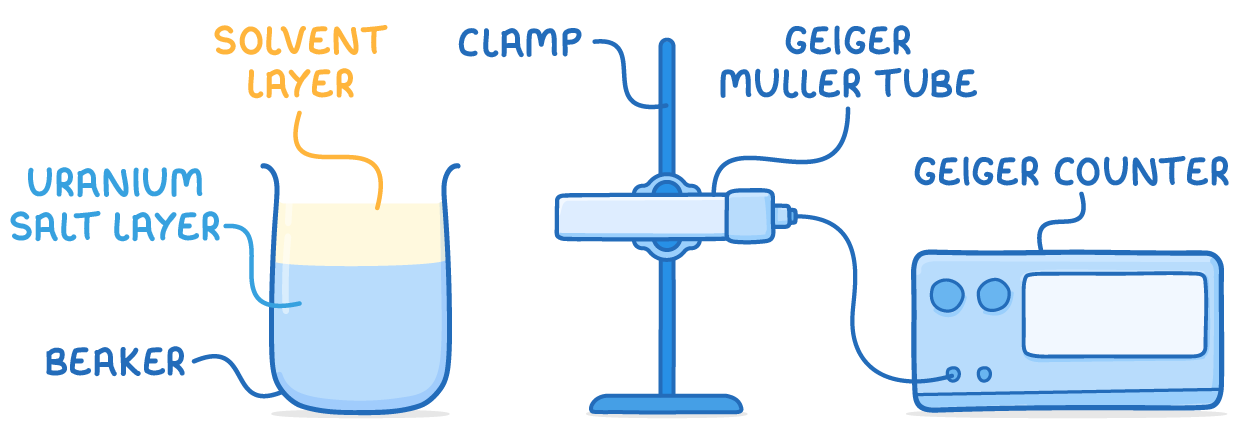
Diagram showing the setup for an experiment with uranium salt and a Geiger counter to measure decay count rate, including a beaker with solvent and uranium salt layers, a clamp, a Geiger Muller tube, and a Geiger counter.

A common experiment involves using uranium salts to produce protactinium-234, then measuring its decay count rate over time.


Method:

  1. Mix uranium salt with solvents then wait for layer separation
  2. Position Geiger counter to detect decays from top solvent layer
  3. Record count rate continuously from time of separation
  4. Plot count rate values against time to obtain decay graph
  5. Use decay graph to determine half-life as count rate reduces