Diffraction Gratings

This lesson covers: 

  1. The impact of increasing the number of slits on the sharpness of interference patterns
  2. How diffraction gratings can be used to measure the wavelength of light
  3. The relationship between wavelength, grating properties, and the angle of diffraction
  4. The way a diffraction grating separates white light into a spectrum of colours

The effect of more slits on interference patterns

Comparison of interference patterns from double slit and diffraction grating.

Adding more slits enhances the resulting interference pattern:

  • Increasing the number of slits results in more light beams contributing to the interference pattern.
  • This enhancement leads to brighter and narrower bright fringes.
  • Conversely, the dark fringes become more pronounced and darker.

With hundreds of slits per mm, diffraction gratings create very distinct and sharp interference fringes.


These sharper fringes are crucial for making more accurate measurements of light properties like wavelength.

Measuring light wavelength with a diffraction grating

Diagram showing the diffraction of laser light through a grating producing zero central order first order second order and third order lines on a screen.

A diffraction grating can produce sharp, well-defined bright fringes at particular angles when monochromatic light is used. Some important features of this pattern include:

  • The central maximum is known as the zero-order line.
  • The first bright lines on either side of this central line are the first-order lines.
  • Further out are the second-order lines, and so on.


The wavelength of light can be determined using the spacing of these fringes and simple geometry, using the formula:


dsinθ=nλ


Where:

d = distance between adjacent slits (m)

θ =angle formed with the normal to the grating at the nth order fringe (°)

λ = wavelength (m)


A larger wavelength (λ) results in a larger angle of diffraction (θ).

As a result, the interference pattern spreads out more, with fewer lines per unit length visible.

Worked example - Calculating wavelength using a diffraction grating

A diffraction grating has a slit spacing of 1.2 x10-6 m. The first order maximum forms an angle of 30° to the zero order. Calculate the wavelength of light used.


Step 1: Formula

dsinθ=nλ


Step 2: Rearrangement

λ=ndsinθ​


Step 3: Substitution and correct evaluation

λ=11.2×10−6 × sin(30)​=6×10−7 m = 600 nm

How White Light is Separated into a Spectrum

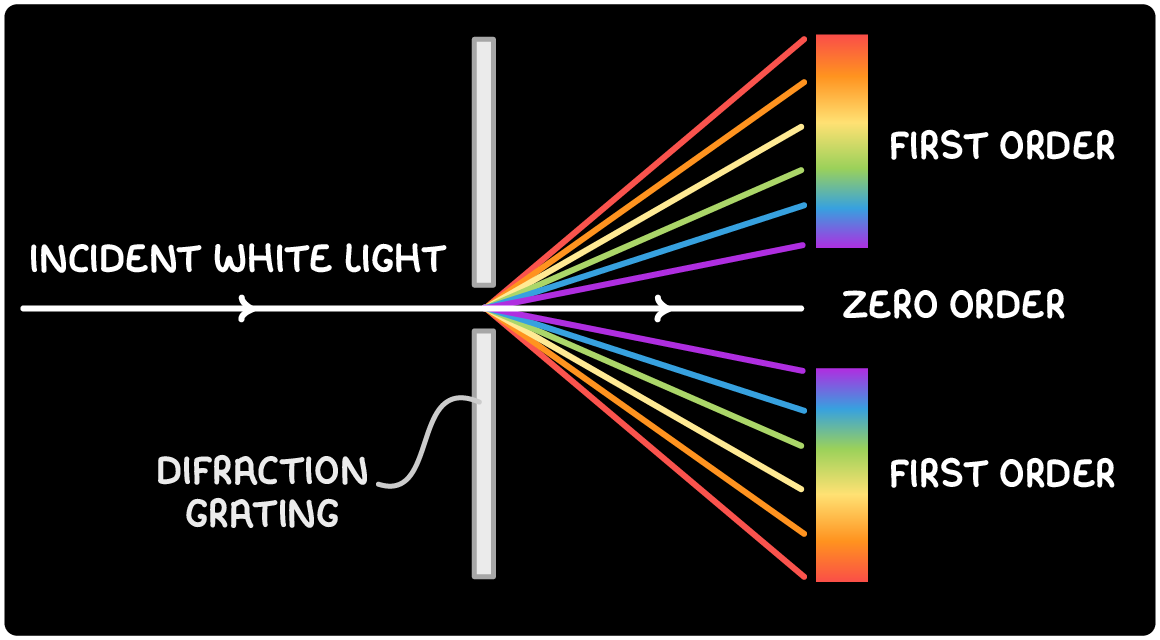
Diagram showing how white light is separated into a spectrum through a diffraction grating.

When white light, which contains a mix of all visible wavelengths, passes through a diffraction grating, it separates into its component colours:

  • Each order of the spectrum displays a range of colours from red to violet.
  • The central, zero-order line remains white, as it combines all wavelengths.