Progressive Waves

This lesson covers: 

  1. Definition of a wave
  2. Describing waves using displacement, amplitude, wavelength, period and frequency
  3. Definitions of transverse and longitudinal waves
  4. Relationship between frequency and time period
  5. The wave equation linking velocity, frequency and wavelength

Waves

A wave is a repeated vibration which transfers energy from one point to another without transferring matter.

Waves can be reflected, diffracted and diffracted.


Waves can be categorised as:

  • Progressive - A wave where energy is transferred from one point to another without transferring matter.
  • Stationary - A wave where there is no net energy transferred from one point to another.

Transverse waves

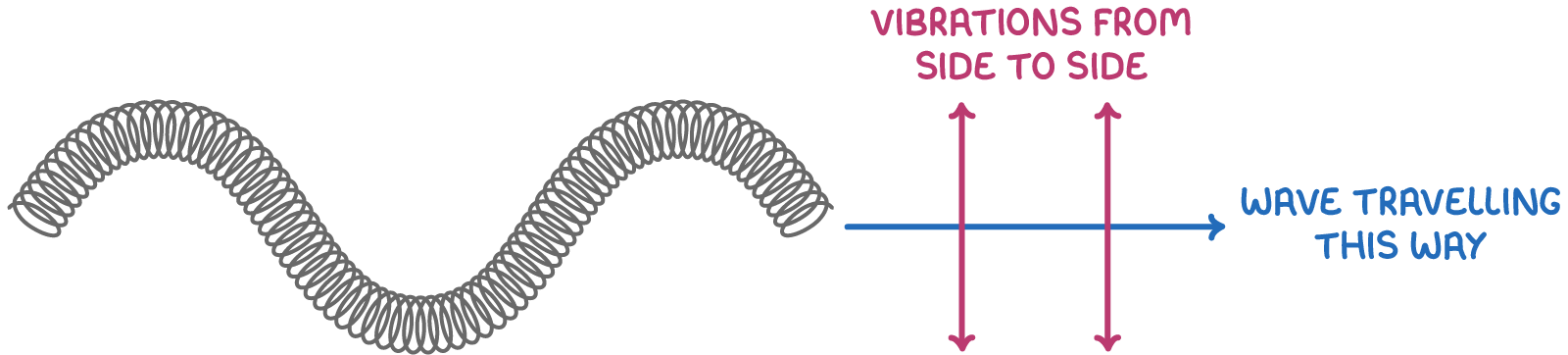
Diagram showing a transverse wave with vibrations from side to side and wave travelling direction.

Transverse waves has oscillations which are perpendicular to the direction of wave travel.


The diagram below shows some key features of a transverse wave.

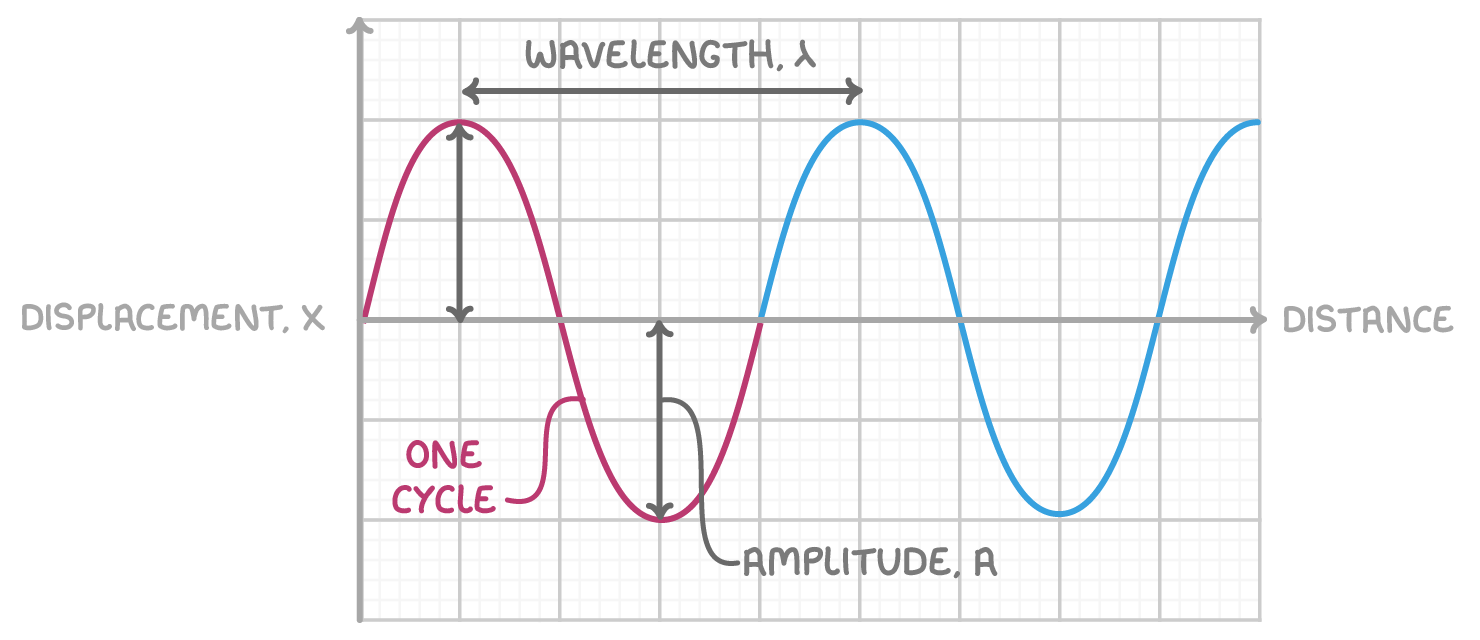
Diagram showing the key features of a transverse wave including displacement, amplitude, and wavelength.
  • Displacement (x) - How far a wave has travelled from its equilibrium position, measured in metres (m)
  • Amplitude (A) - Maximum displacement from the equilibrium position, measured in metres (m)
  • Wavelength (λ) - The length of one complete wave, measured in metres. Wavelength can be measured as the distance between consecutive peaks.


Examples of transverse waves include:

  • All electromagnetic waves (light)
  • Water waves
  • Waves on strings
  • Earthquake shock wave (S-wave)

Longitudinal waves

Longitudinal waves have oscillations which are parallel to the direction of wave travel.

Diagram showing longitudinal waves with labels for compression, rarefaction, one wavelength, and direction of wave travel.
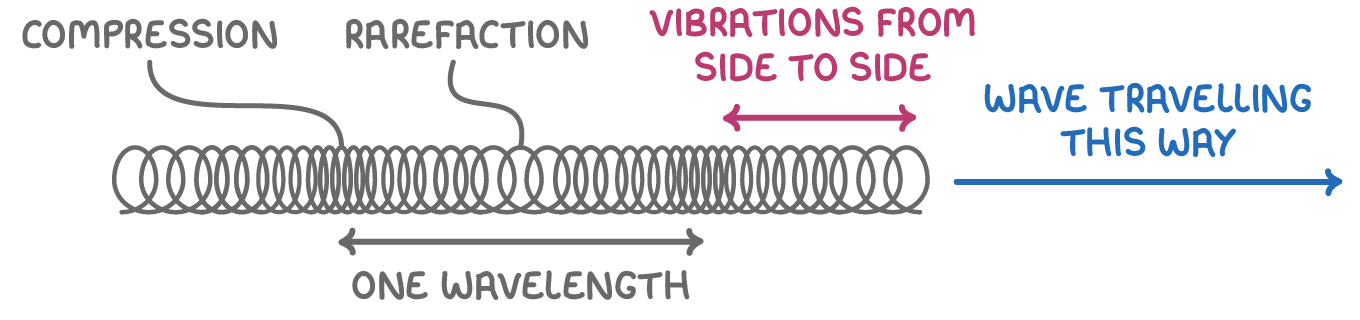
  • Compressions - region where the particles are closest together.
  • Rarefaction - region where the particles are furthest apart.
  • Wavelength (λ) - length of one wave, measured from the centre of one compression to the centre of the next compression. Wavelength is measured in metres (m).

Relating frequency and period

The time taken for one complete wave is known as the time period (T), measured in seconds (s).

The frequency of a wave is defined as the number of complete waves per second, measured in Hertz (Hz).

The time period and frequency of a wave are related by:


f = T1​


Where:

f = frequency (Hz)

T = time period (s)

The wave equation

The speed of a wave depends on both the frequency and wavelength of a wave:


v = f λ


Where:

v = wave speed (m s−1)

f = frequency (Hz)

λ = wavelength (m)

Worked example: Calculating wave speed

Calculate the wave speed of a wave which has a frequency of 250 MHz and a wavelength of 1.2 m.


Step 1: Equation

v = f λ


Step 2: Convert MHz into Hz

to convert from MHz to Hz, multiply by 1 x 106

250 MHz = 250 x 106 Hz


Step 3: Substitution and correct evaluation

v = f λ

v=250×106×1.2=3×108 m s−1