Conservation Of Energy

This lesson covers: 

1. The concept of kinetic energy and how to calculate it
2. Gravitational potential energy due to an object's position
3. The law of conservation of energy
4. An example applying energy concepts to a pendulum system

Kinetic Energy

Kinetic energy is the energy that an object possesses due to its motion. To calculate the kinetic energy of an object, use the formula:

Ek​=21​m v2

Where:

E_k = kinetic energy (J)

m = mass (kg)

v = speed (m s^-1)

Worked example - Kinetic energy of a rolling ball

Calculate the kinetic energy of a ball rolling with a velocity of 5 m s^-1 and a mass of 2 kg.

Step 1: Formula

Ek​=21​ m v2

Step 2: Substitution and Correct evaluation

Ek​=21​×2×52=21​×2×25=25 J

Gravitational potential energy

Gravitational potential energy is the energy stored in an object as a result of its vertical position within a gravitational field.

It is calculated using the formula:

Ep​ = m g h

Where:

• m = mass (kg)
• g = acceleration due to gravity (9.81 m s^-2).
• h = height above reference point (m).

Worked Example - Gravitational potential energy of a raised ball

Let's calculate the gravitational potential energy of a ball that weighs 1 kg and is raised to a height of 10 meters.

Step 1: Formula

Ep​ = m g h

Step 2: Substitution and correct evaluation

Ep​=1×9.81×10=98.1 J

Conservation of mechanical energy

The law of conservation of energy states that energy is only transformed from one type to another; it is neither created nor destroyed.

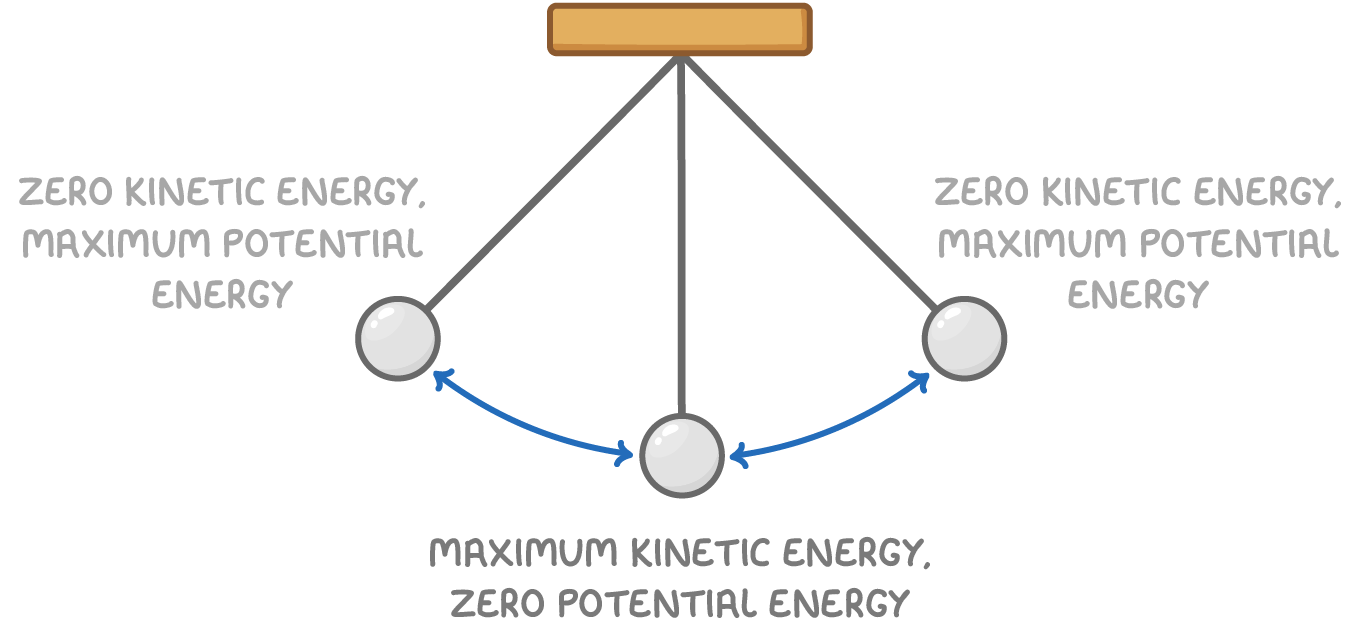
In the case of a pendulum, the total mechanical energy is maintained throughout its motion. As it swings, the pendulum's energy constantly transforms between kinetic energy and potential energy.

Key points:

• At the highest points of its swing, the pendulum has maximum potential energy and minimum kinetic energy.
• At the lowest point of its swing, the pendulum has maximum kinetic energy and minimum potential energy.