Hooke's Law

This lesson covers: 

1. How Hooke's Law relates the extension of an object to an applied force
2. Experimental procedure to investigate Hooke's Law
3. The application of Hooke's Law to springs and other materials
4. The limits of proportionality and elasticity for materials following Hooke's Law
5. Combining Hooke's Law for objects arranged in parallel or in series
6. Differences between elastic and plastic deformation

Hooke's law for wires and springs

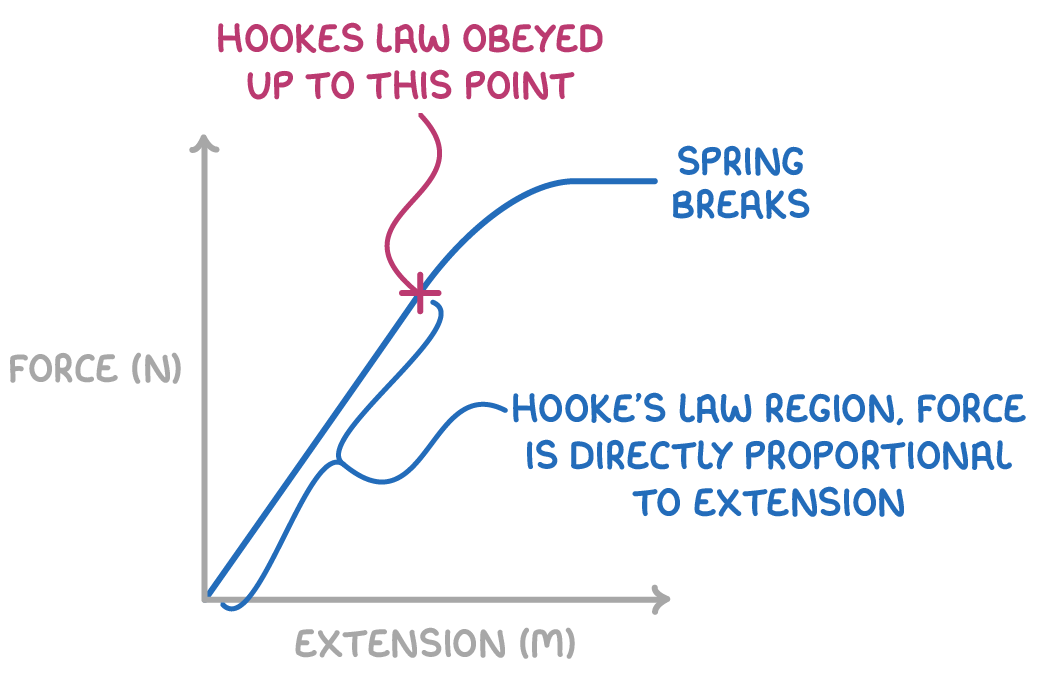
Hooke's law states that the extension of an object is directly proportional to the force applied, provided the force does not exceed the elastic limit.

This can be expressed as:

F = k x

Where:

F = applied force (N)

k = spring constant (N m−1)

x = extension (m)

This law applies to springs as well as other materials like wires and rubber bands.

Experimental investigation of Hooke's law

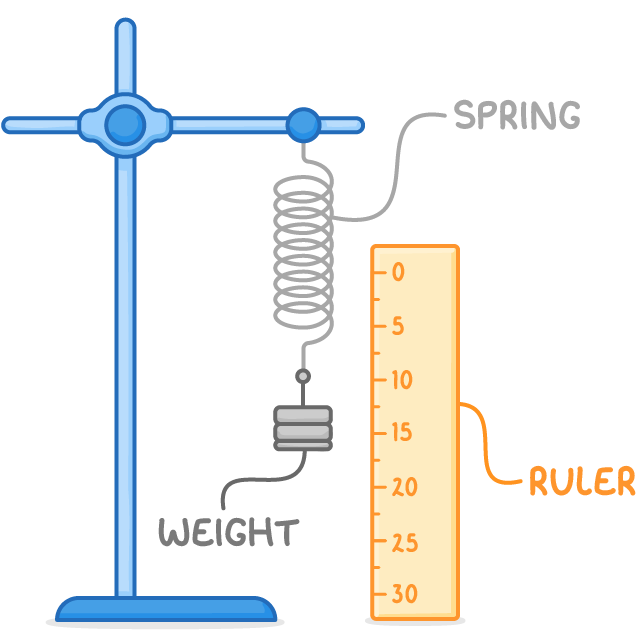
To experimentally verify Hooke's Law:

1. Clamp the spring at the top and measure its original length
2. Incrementally add weights, measuring the new length each time
3. Calculate extension by subtracting the original length from the extended length
4. Plot force vs extension

Note: Where the graph shows a linear relation, Hooke's Law applies.

Elastic vs plastic deformation

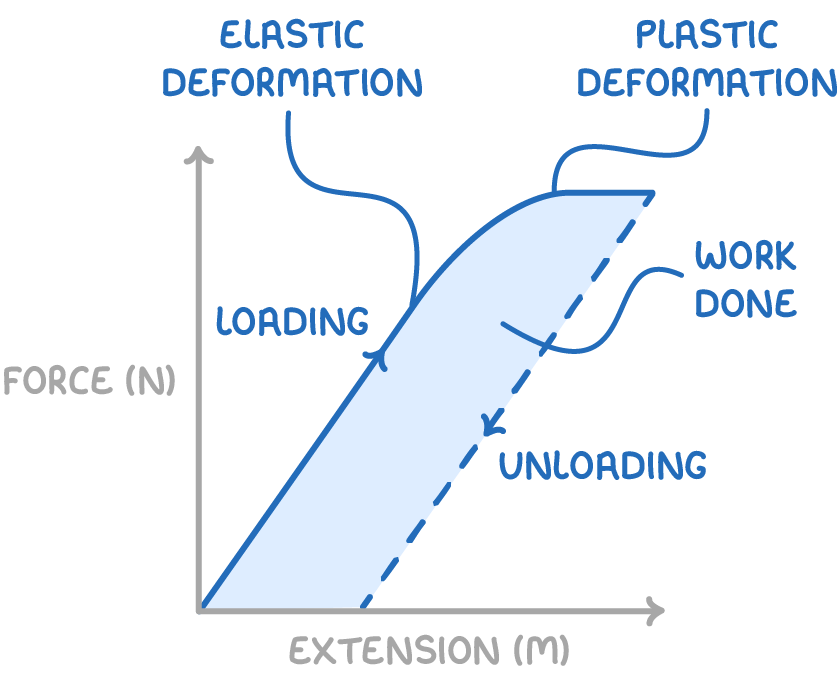
Whether a material deformation is elastic or plastic depends on if the material returns to its original shape when the force is removed:

• Elastic deformation - When the applied force is removed, the material returns to its original shape and size.
• Plastic deformation - When the applied force is removed, the material remains partially deformed.

In elastic deformation, the atoms briefly move apart then revert back to their equilibrium positions.

In plastic deformation, the relative positions of atoms change permanently.

Springs in series and parallel

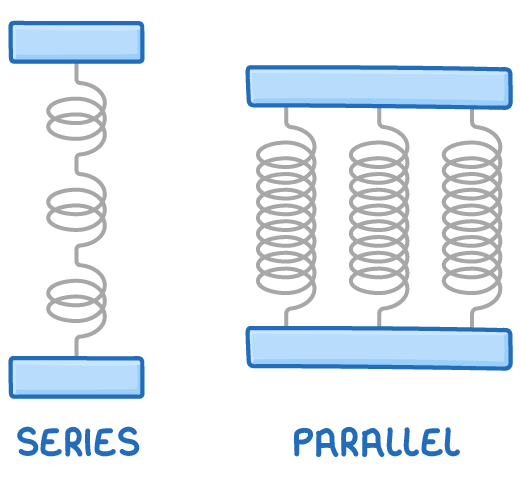
For springs arranged in series or parallel, an equivalent spring constant (k) can be calculated by combining the individual spring constants:

Springs in series:

k=k1​1​+k2​1​+k3​1​+...+kn​1​1​

Springs in parallel:

k=k1​+k2​+k3​+...+kn​

Where:

k = equivalent spring constant (N m^-1)

k₁ = spring constant of spring 1 (N m^-1)

k₂ = spring constant of spring 2 (N m^-1)

k₃ = spring constant of spring 3 (N m^-1)

k_n = spring constant of the n^th spring (N m^-1)

Worked example - Determining the combined spring constant in parallel and series

A student has three springs with spring constants k₁ = 300 N m^-1, k₂ = 400 N m^-1, and k₃ = 500 N m^-1.

Calculate the equivalent spring constant when these springs are combined in series and in parallel.

Part 1: Springs in series

Step 1: Formula for springs in series

ktotal​1​=k1​1​+k2​1​+k3​1​1​=0.00783

Step 2: Substitution and correct evaluation

ktotal​1​=3001​+4001​+5001​1​=0.00783

ktotal​ = 127.7 N m−1

Part 2: Springs in Parallel

Step 1: Formula for springs in parallel

ktotal​=k1​+k2​+k3​

Step 2: Substitution and correct evaluation

ktotal​=300+400+500=1200N m−1