Capacitor Charge & Discharge

This lesson covers: 

  1. Charging capacitors using DC power supplies
  2. Discharging capacitors when disconnected
  3. Exponential decrease of charge during discharge
  4. Calculating charge, current and potential difference over time
  5. Defining the time constant

Charging a capacitor

For charging, we connect capacitors in a circuit that includes a DC power supply, an ammeter, and a voltmeter.

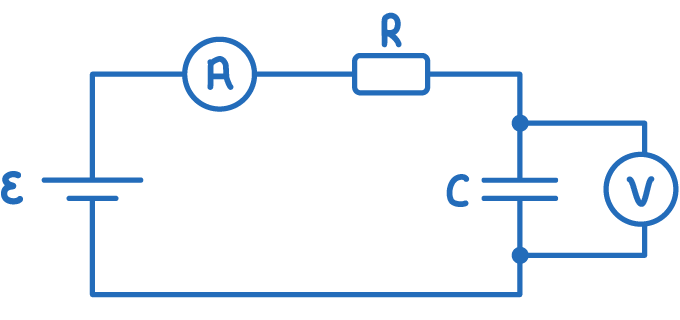
Diagram showing a circuit for charging a capacitor with a DC power supply, ammeter, voltmeter, and resistor.

Initially, the capacitor charges quickly, with a high current flowing into it. Over time, as more charge accumulates, it becomes increasingly difficult to add more electrons due to the repulsive force between the like charges. This results in the current decreasing exponentially. The capacitor is considered fully charged when the potential difference across it matches that of the power supply, leading to zero current flow.

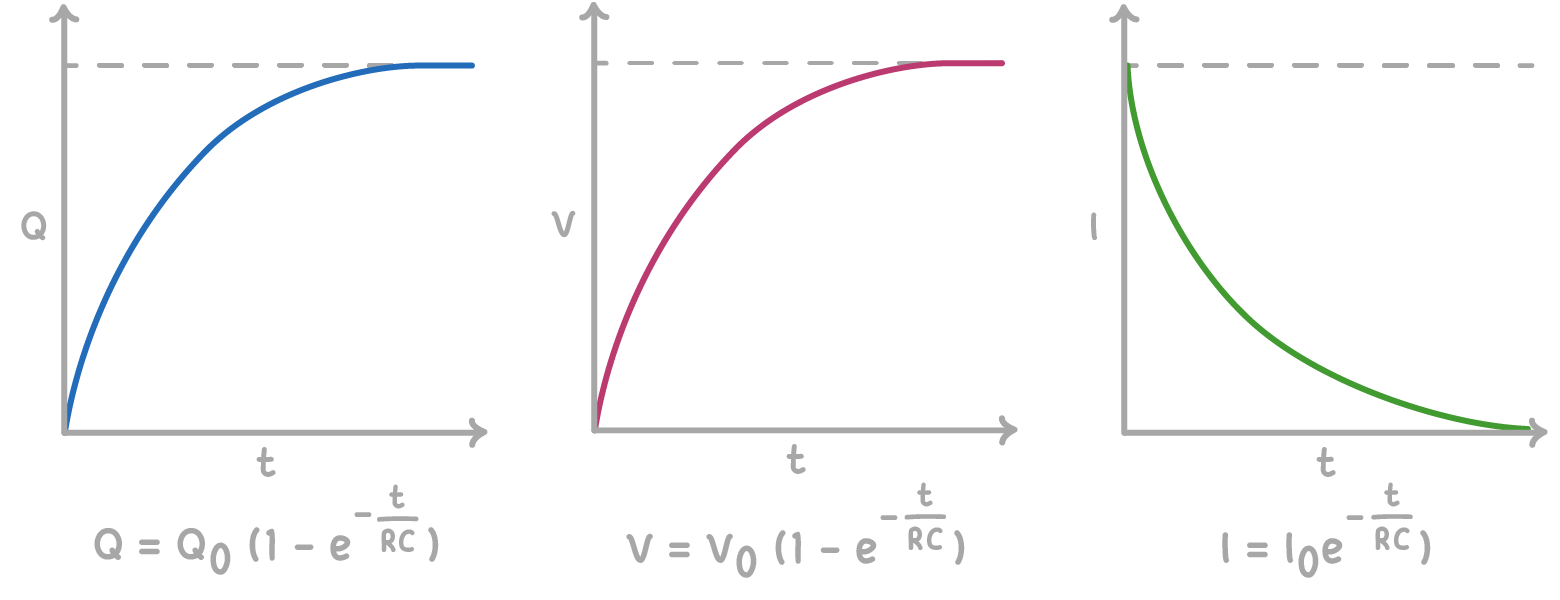
Graphs showing charge, voltage, and current over time for a charging capacitor.

Where:

  • Q = charge at time t (C)
  • Q0 = charge when fully charged (C)
  • V = voltage at time t (V)
  • V0 = voltage when fully charged (V)
  • I = current at time t (A)
  • I0 = initial current (A)
  • t = time (s)
  • R = resistance (Ω)
  • C = capacitance (F)

Worked example - Calculating charge on a capacitor after a given time

Consider a capacitor with a capacitance of 5 μF, connected in a circuit with a 10 kΩ resistor. Calculate the charge on the capacitor 0.15 seconds after the charging process begins, given an initial DC power supply voltage of 12 V.


Step 1: Calculate Q0

Q0 is the charge stored by the capacitor when fully charged.

Q0 = V0 C

Q0 = 12 x 5 x 10-6 = 6 x 10-5 C


Step 2: Formula for charging capacitor

Q = Q0​×(1−e−R Ct​)


Step 3: Substitution and correct evaluation

Q=6×10−5(1−e−10,000×5×10−60.15​)=5.7×10−5 C

Defining the time constant (τ)

The time constant, denoted as τ, is a product of resistance (R) and capacitance (C) in the circuit.


τ = R C


Where:

τ = time constant (s)

R = resistance (Ω)

C = Capacitance (F)


It is important because:

  • τ represents the time it takes for the capacitor to reach approximately 63% of its maximum charge or voltage during charging or discharging.
  • 5τ is roughly the time needed for a capacitor to fully charge or discharge.


Hence, the greater the resistance or capacitance, the longer the time constant, which in turn slows down the charging and discharging processes.

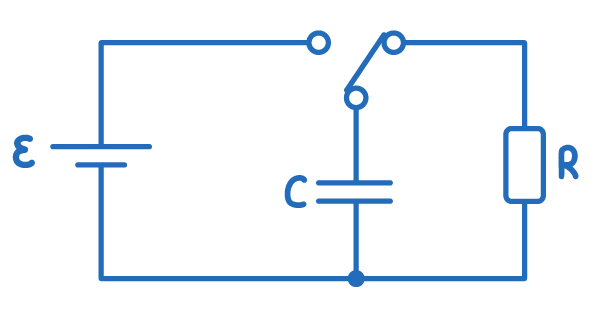
Discharging a capacitor

To discharge a capacitor:

  1. Disconnect it from the power supply.
  2. Connect its terminals together.


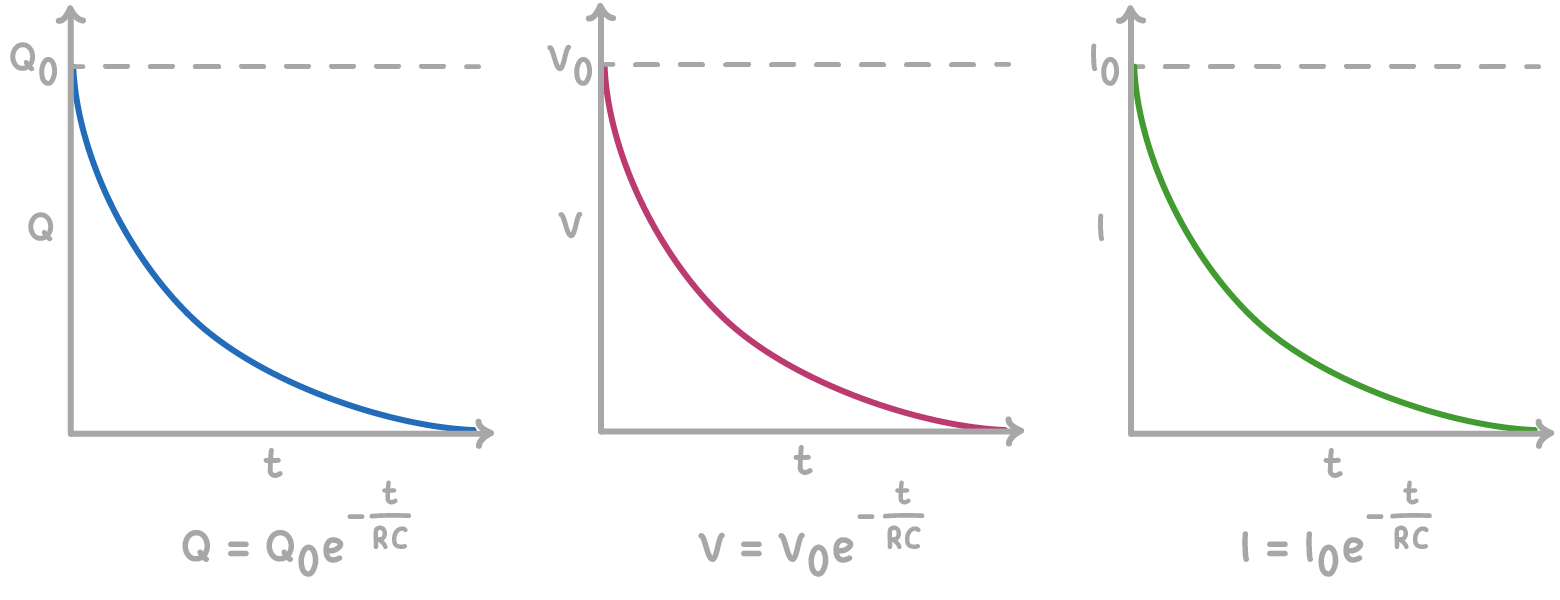
This allows the stored charge to flow out of the capacitor, back through the circuit. Similar to charging, the discharge current and the voltage across the capacitor both start high and decrease exponentially until the capacitor is fully discharged.

Circuit diagram showing the discharge of a capacitor with a resistor in the circuit.

The amount of charge, voltage and current at any given time 't' during discharge is described by exponential decay equations.

Graphs showing the exponential decay of charge, voltage, and current during capacitor discharge.

Worked example: - Calculating the remaining voltage across a discharging capacitor

Consider a 470 μF capacitor initially charged to 10 V, now discharging through a 4 kΩ resistor. Calculate the voltage across the capacitor after 5 seconds.


Step 1: Formula for Discharging Capacitor

V = V0​×e−R Ct​


Step 2: Substitution and correct evaluation

V = 10× e−4,000×470×10−65​ = 2.66 V