Newton's Law

This lesson covers: 

  1. Understanding that the gravitational force is always attractive and depends on the masses involved and the distance between them.
  2. Using Newton's law of gravitation to calculate the force between two masses.
  3. Recognising that Newton's law of gravitation follows an inverse square relationship.

Gravitational force is always attractive

The gravitational force experienced by any object in a gravitational field is invariably attractive. This force, a vector quantity, is influenced by two primary factors:

  • The masses of the two interacting objects.
  • The distance between the centres of these objects.

Calculating Gravitational Force Using Newton's Equation

The gravitational force between two uniform spheres, which can be approximated as point masses, is computed using Newton's law of gravitation, represented by the formula:


F = = r2G M m​


Where:

  • F = Gravitational force (N)
  • G = Gravitational constant (6.67 x 10-11 N m2 kg-2)
  • M, m = Masses of the objects (kg)
  • r = Distance between the centres of the masses (m)

Worked example - Calculating gravitational force between the Earth and the Moon

Calculate the gravitational force between the Earth and the Moon. The Earth has a mass of 5.97 x 1024 kg and the Moon has a mass of 7.35 x 1022 kg. The average distance between the centres of the Earth and Moon is 3.84 x 108 meters.


Step 1: Formula

F = r2G M m​


Step 2: Substitution and correct evaluation

F = (3.84×108)26.67×10−11×5.97×1024×7.35×1022​=1.99×1020 N

Newton's Law Follows an Inverse Square Relationship

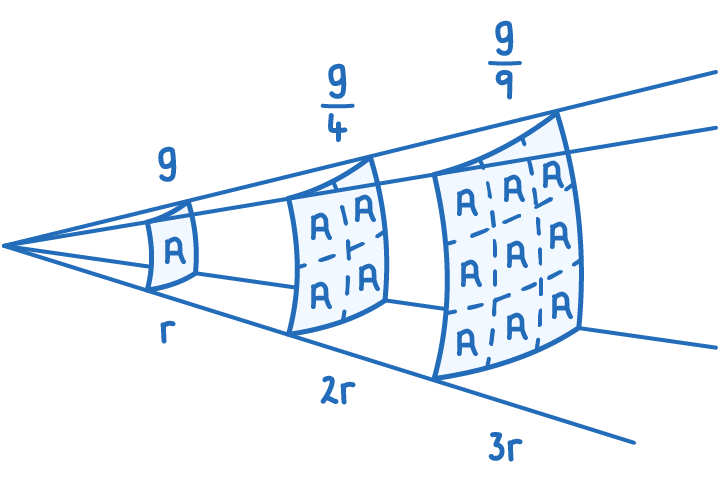
Illustration showing the inverse square relationship in Newton's law of gravitation with force decreasing as distance increases.

Newton's law of gravitation is characterised by an inverse square relationship. If the distance between two masses doubles, the gravitational force decreases to one quarter of its original value.