Pressure, Volume & Temperature Equations Lesson | GCSE Physics SQA5

Pressure, Volume & Temperature Equations

This lesson covers:

The idea that pressure multiplied by volume is constant, at a fixed temperature
The gas equations : $pV=\text{constant}$ , and $p$
The idea that pressure divided by temperature is constant, at a fixed volume
The gas equations: $\frac{p}{T}=\text{ constant }$ and $\frac{p$

When kept at a constant temperature, the pressure and volume of a gas are proportional.

inversely

For a gas at a constant temperature, which statements are true?

(Select all that apply)

When volume decreases, pressure decreases

When volume increases, pressure decreases

When volume decreases, pressure increases

When volume increases, pressure increases

Which is the correct formula for the relationship between pressure and volume, at constant temperature?

pressure x volume = constant

pressure x volume = temperature

pressurevolume = constant

volumepressure = constant

For a gas at constant temperature, pressure x volume always equals the same constant. Therefore:

$p$

Where:

$p$ $1$ is the initial pressure

$V$ $1$ is the initial volume

$p$ $2$ is the pressure after a change occurs

$V$ $2$ is the volume after a change occurs

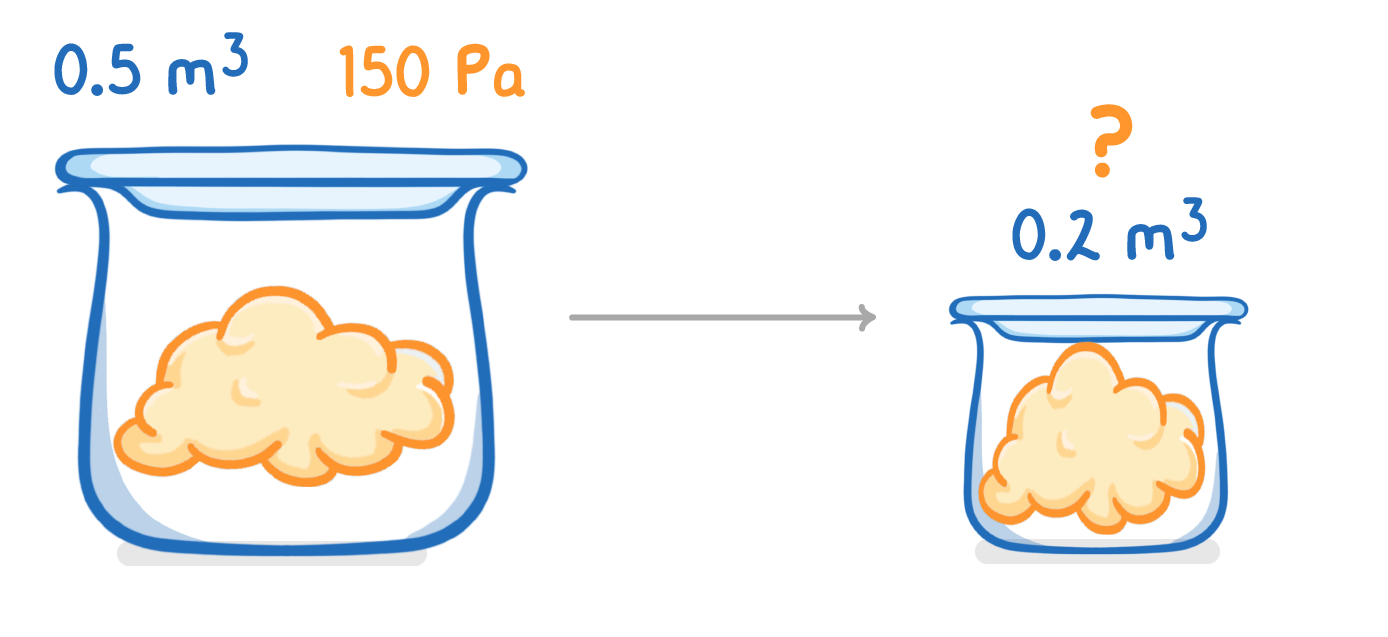
Diagram showing a gas occupying a volume of 0.5 cubic meters at a pressure of 150 pascals and being compressed to 0.2 cubic meters with a question mark indicating the unknown pressure.

A gas occupies a volume of 0.5 m³ at a pressure of 150 Pa.

Calculate the pressure exerted by the gas if the volume is compressed to 0.2 m³?

(Assume constant temperature)

375

A gas occupies a volume of 0.3 m³ at a pressure of 50 Pa.

The pressure increased to 150 Pa, what is the new volume?

(Assume constant temperature)

0.1

m³

A gas initially occupied a volume of 10 L at an unknown pressure.

The gas was then compressed to 2 L, and measured as having a pressure of 20 kPa.

Calculate the original pressure before the gas was compressed.

(Assume constant temperature)

kPa

At a constant volume

Tp= constant

This formula works in a very similar way to the one in the video, but is at a constant volume rather than a constant pressure. It leads to the formula:

T1p1=T2p2

What makes this formula complicated is that the temperature has to be in Kelvin rather than Celsius. This means that you have to add 273 to any Celsius temperature value.

For example:

0°C + 273 = 273 K

25° + 273= 298 K

100°C + 273 = 373 K

A solid container is filled with a gas at a pressure of 100 kPa and a temperature of 150 K. The container (and gas inside it) is then heated to a temperature of 240 K.

Assuming a constant volume, calculate the new pressure after the gas has been heated.

160

kPa