Elastic Potential Energy Lesson | GCSE Physics OCR 21st Century Higher Triple

Elastic Potential Energy

This lesson covers:

1The elastic force equation: $F=ke$

2The elastic potential energy equation: $Ee=\frac{1}{2}ke2$

3How to interpret force-extension graphs

lower / higher / spring

Every spring has a characteristic called the constant, which is a measure of how firm the spring is.

A spring constant means the spring is more firm.

A spring constant means the spring is less firm.

spring

higher

lower

0

/

3

The formula that links force and extension is:

F = $ke2$

$F\ =\ \frac{W}{d}$

$F\ =\ ke$

$F\ =\ \frac{1}{2}ke2$

0

/

1

A spring has a spring constant of 120 N/m, and an unstretched length of 0.5m.

What force is required to stretch the spring from 0.5m, to 0.6m?

12 N

72 N

60 N

1,200 N

0

/

1

A force of 5 N is applied to a spring, causing it to stretch from a length of 0.1 m, to a length of 0.15 m.

What is the spring constant of the spring?

50 N/m

0.25 N/m

33.3 N/m

100 N/m

0

/

1

Illustration of a stretched spring representing elastic potential energy.

When a spring is stretched, energy is transferred to its potential energy store.

Then when the spring is released, most of that energy is transferred to energy.

elastic

kinetic

0

/

2

The formula for elastic potential energy is:

$Ee\ =\ \frac{1}{2}ke2$

$Ee\ =\ ke$

$Ee\ =\ \frac{1}{2}ke$

$Ee\ =\ ke2$

0

/

1

A spring with a spring constant of 4 N/m is stretched by 0.5 m.

How much elastic potential energy did it gain?

0.5|1\div 2|\frac{1}{2}

J

0

/

1

8 J of energy is used to stretch a spring by 0.1 m.

What is the value of its spring constant?

1600

N/m

0

/

1

Below is a force-extension graph for a typical spring.

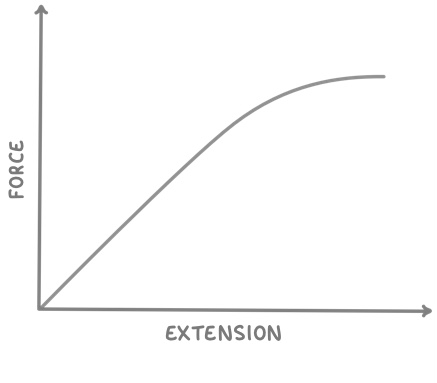Force-extension graph for a typical spring showing linear and curved regions.

The gradient of the straight part of the graph tells us the:

Elastic potential energy

Elastic limit

Limit of proportionality

Spring constant

[0/1]

The area under the curve tells us the:

Spring constant

Elastic limit

Limit of proportionality

Elastic potential energy

[0/1]

The point where the line goes from straight to curved is referred to as the:

Elastic limit

Limit of proportionality

Elastic potential energy

Spring constant

[0/2]

0

/

4