Moments (Part 2 - Seesaws & Gears) Lesson | GCSE Physics OCR Gateway Higher Triple

Moments (Part 2 - Seesaws & Gears)

This lesson covers:

How levers work
How gears work

Levers work by transmitting the turning effect of a force.

Levers use the principle of moments.

What formula do we use to calculate a moment?

$M=ke$

$M=Fd$

$M=Fe$

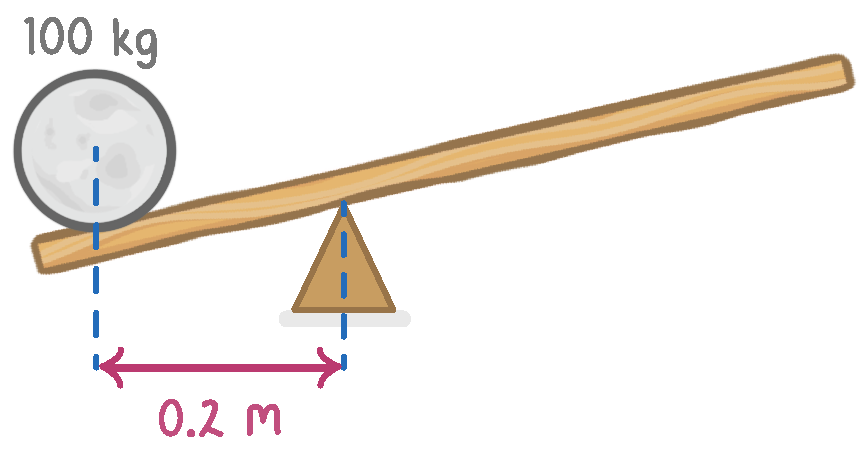Diagram showing a 100 kg rock placed 0.2 m from the pivot on a lever.

A big rock has a mass of 100 kg and is placed on a lever 0.2 m from the pivot.

To recap, the formula for weight is:

$W=\frac{m}{g}$

$W=Fd$

$W=mg$

[0/1]

What is the weight of the 100 kg rock?

The gravitational field strength on earth is 9.8 N/kg

980

[0/1]

The rock has a weight of 980 N and is 0.2 m from the pivot. What is the size of the moment generated by the rock?

196

[0/1]

Which direction is the moment generated by the rock?

Clockwise

Anti-clockwise

[0/1]

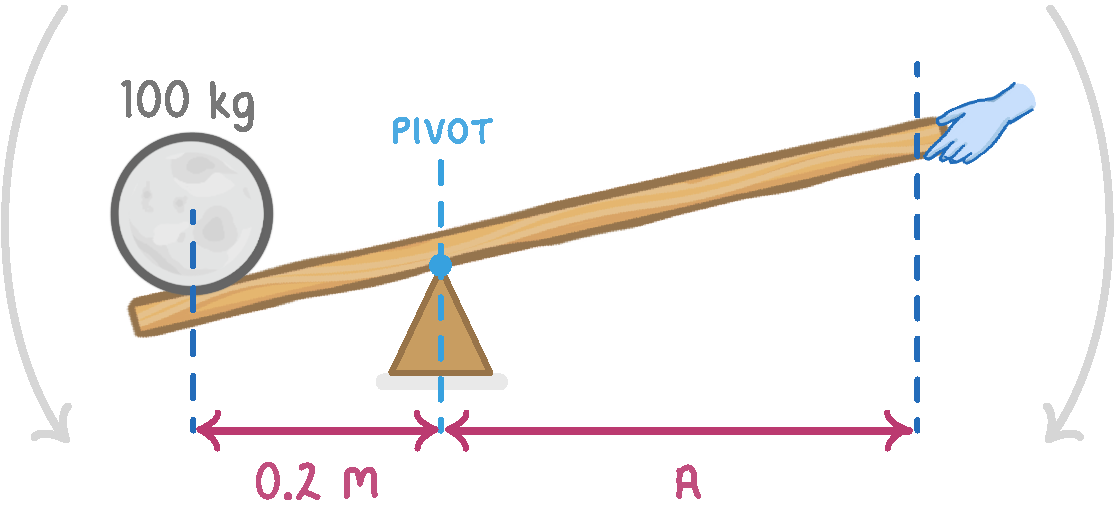Diagram showing a 100 kg rock on a lever 0.2 m from the pivot with a person applying force on the other side.

A person can push down with a force of 400 N on the other side of the lever.

To lift the rock, the person must generate a moment that is greater than the moment generated by the rock.

The rock generates an anti-clockwise moment of 196 Nm. Therefore, the person must generate a clockwise moment greater than 196 Nm.

Rearrange the moment equation to make distance the subject:

d=FM

d=MF

[0/1]

The distance 'A' in the diagram above is the perpendicular distance between the 400 N downward force, and the pivot.

Applying the force further than the distance 'A' will lift the rock.

What is the distance 'A'?

0.49

[0/1]

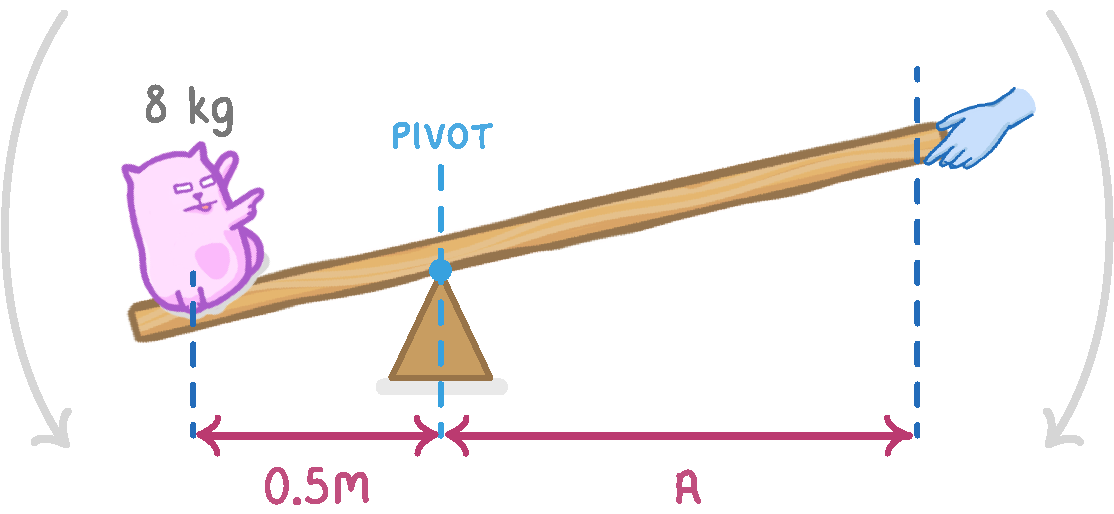
Diagram showing a cat with a mass of 8 kg on a lever 0.5 m from the pivot and a person applying a force of 40 N on the other side.

A cat has a mass of 8 kg and is placed on a lever 0.5 m from the pivot. The gravitational field strength on earth is 9.8 N/kg.

A person pushes down with a force of 40 N on the other side of the lever.

Applying a force further than the distance 'A' will lift the cat.

Calculate the distance 'A'.

(Remember to calculate the weight of the cat)

0.98

When two gears are connected, do the gears turn in opposite directions, or the same direction?

Opposite

Same

The ratio of the turning effect of the two gears is proportional to the ratio of the radius of the two gears.

For example: if the radius of gear B (radius is 5cm) is twice the radius of gear A (radius is 10cm), then the turning effect of gear B is also twice the size of the turning effect of gear A.