Refractive Index & Critical Angles
This lesson covers:
- What 'total internal reflection' is
- What the 'critical angle (C)' is
- The formula sin(C) = 1 ÷ n
Total internal reflection and the critical angle When light travels from a more dense medium to a less dense medium (e.g. from glass to air), it speeds up and is refracted away from the normal. The following 3 diagrams illustrate how the behaviour of a light ray changes, depending on whether the angle of incidence is less than / equal to / greater than a medium's critical angle. Be aware that different materials have different critical angles, depending on the refractive index of that material. |
 If the angle of incidence (i) is less than the critical angle: The light ray is refracted away from the normal. |
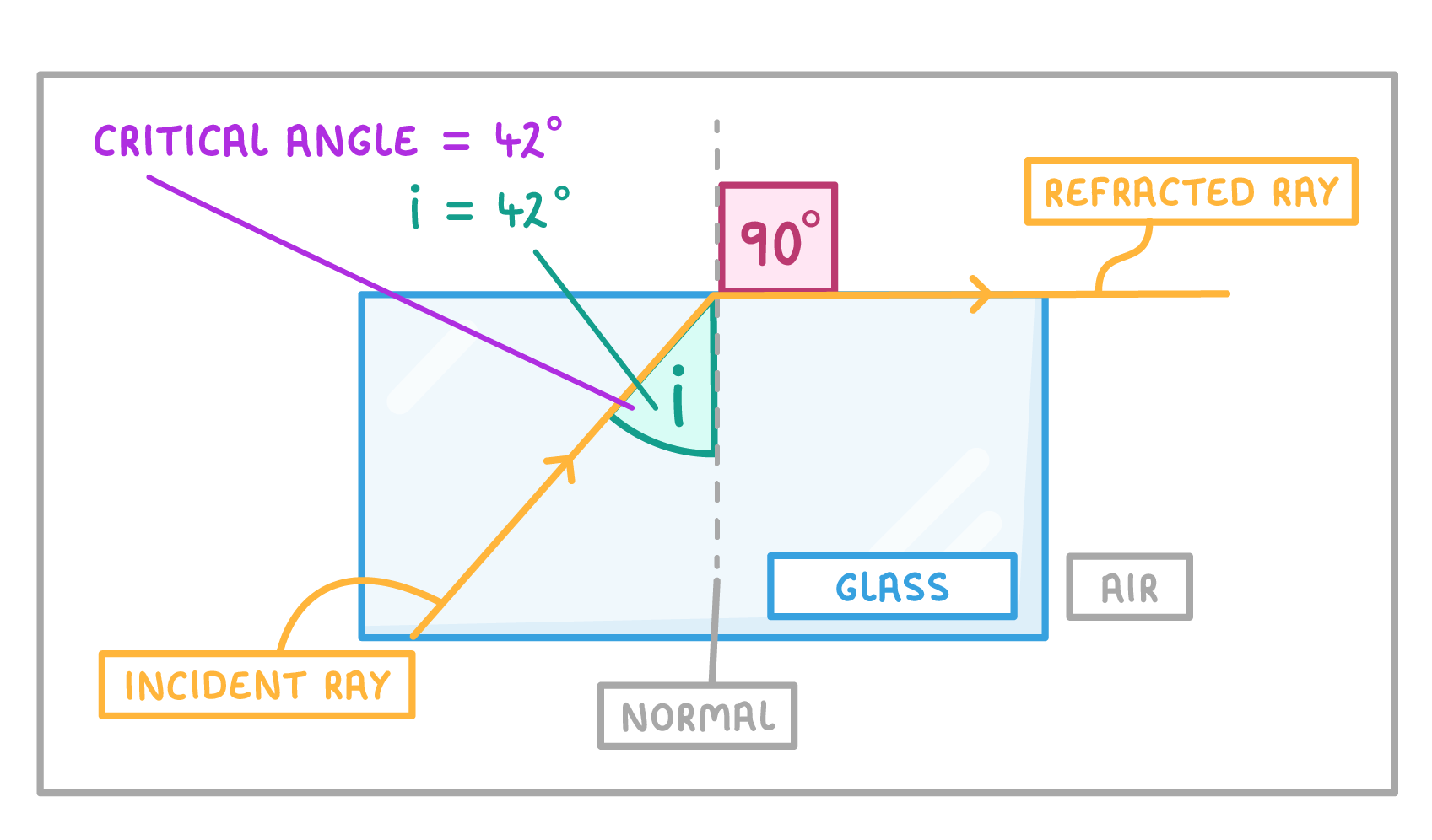 If the angle of incidence (i) is equal to the critical angle: The light ray is refracted at 90° to the normal, and the ray travels along the surface of the denser medium. |
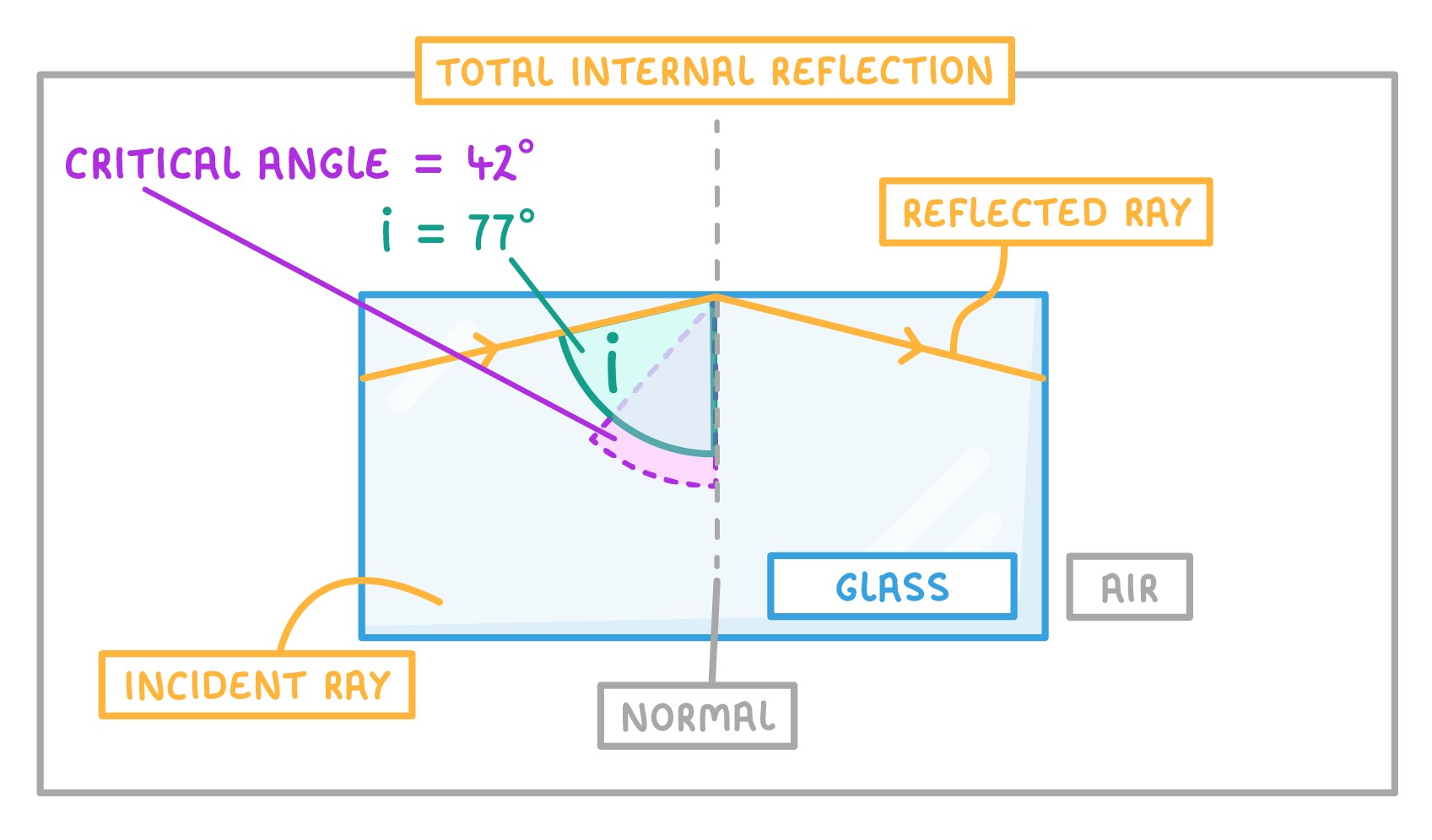 If the angle of incidence (i) is greater than the critical angle: No refraction occurs. All the light is reflected (not refracted) back into the denser medium. This is total internal reflection. |
What name is given to the specific angle of incidence that results in a 90° angle of refraction?
Critical angle
Concise angle
Concave angle
|
Two criteria for total internal reflection
- The rays of light must travel from a more dense medium to a less dense medium (e.g. from glass to air).
- The angle of incidence must be greater than the critical angle.
Critical angle formula
The exact value of the critical angle (C) depends on the refractive index (n) of that specific material.
Finding the critical angle - worked example
The refractive index of water is 1.33. Calculate the critical angle for water, giving your answer to 3 s.f.
The refractive index of diamond is 2.42.
What is the critical angle for diamond? Give your answer to 3 s.f.
°
|
The critical angle for ice is 49.8°.
What is the refractive index for ice? Give your answer to 3 s.f.
|