Moments
This lesson covers:
- What a moment is and how it causes rotation
- How to calculate a moment
- The principle of moments and rotational equilibrium
Forces can cause objects to rotate

A pivot point is the point around which an object rotates in a clockwise or anticlockwise direction, like the middle of a seesaw.
When a force acts on an object that can rotate around a pivot, it creates a turning effect.
This turning effect is called a moment and is measured in newton-metres (Nm).
Calculating moments
The size of the moment depends on two variables:
- Force (F) - measured in newtons (N).
- Perpendicular distance from the pivot (d) - measured in metres (m).
The formula to calculate moments is:
Moment (Nm) = Force (N) × Perpendicular distance from pivot (m)
The greater the force or distance from the pivot, the greater the resulting moment.
Calculating moments example
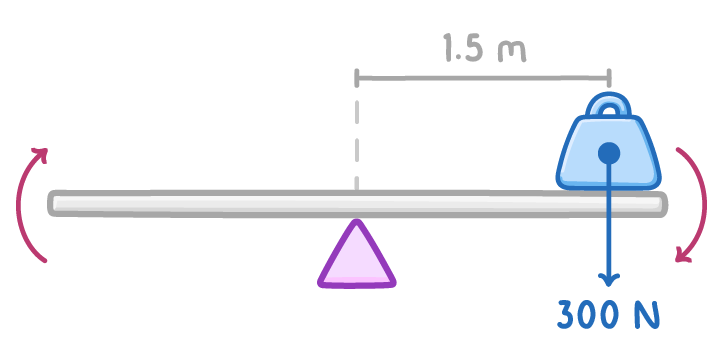
For example a child on a seesaw has a weight of 300 N and a distance of 1.5 m from the pivot.
Step 1: Formula
Moment (Nm) = Force (N) × Perpendicular distance from pivot (m)
Step 2: Substitution
Moment (Nm) = 300 × 1.5
Step 3: Correct evaluation
Moment (Nm) = 300× 1.5 = 450 Nm
Moment = 450 Nm in a clockwise direction.
Balanced and unbalanced moments
For an object to be stable and remain stationary when rotated on a pivot, the sum of anticlockwise moments must equal the sum of clockwise moments.
When moments are balanced, there is no net rotational effect.
Unbalanced moments result in rotation around the pivot.
Balanced moments means no rotational movement
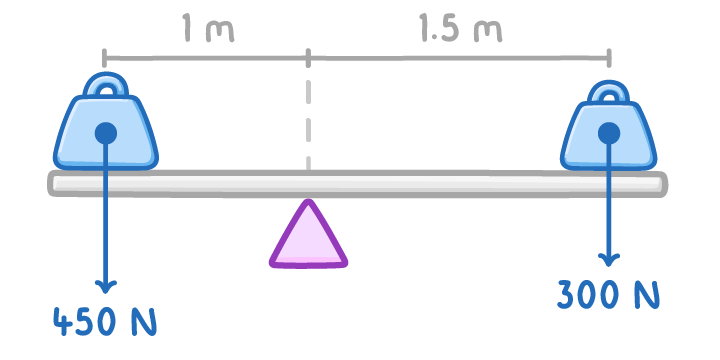
Anti-clockwise moment:
moment = 450 x 1 = 450 Nm
Clockwise moment:
moment = 300 x 1.5 = 450 Nm
The anticlockwise moment = the clockwise movement so there is no rotational movement.
Unbalanced moments means there is rotational movement
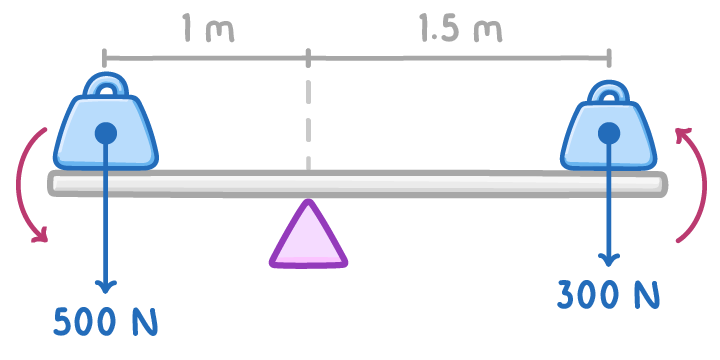
Anticlockwise moment:
moment = 500 x 1 = 500 Nm
Clockwise moment:
moment = 300 x 1.5 = 450 Nm
The anticlockwise moment is greater than the clockwise moment so the seesaw moves anticlockwise around the pivot.