Tree Diagrams

This lesson covers:

  1. What tree diagrams are 
  2. How to use tree diagrams 

Probability tree diagrams


Probability tree diagrams show the probabilities of a set of events. To create them you put the events at the end of each branch, and the probabilities of those events on the branches.

Example:


Tom is going to play one squash match and one badminton match. The probability that he will win the squash match is 4/5. The probability that he will win the tennis match is 2/3.


What is the probability that he will only win one of the games?

Step 1: Construct a probability tree diagram.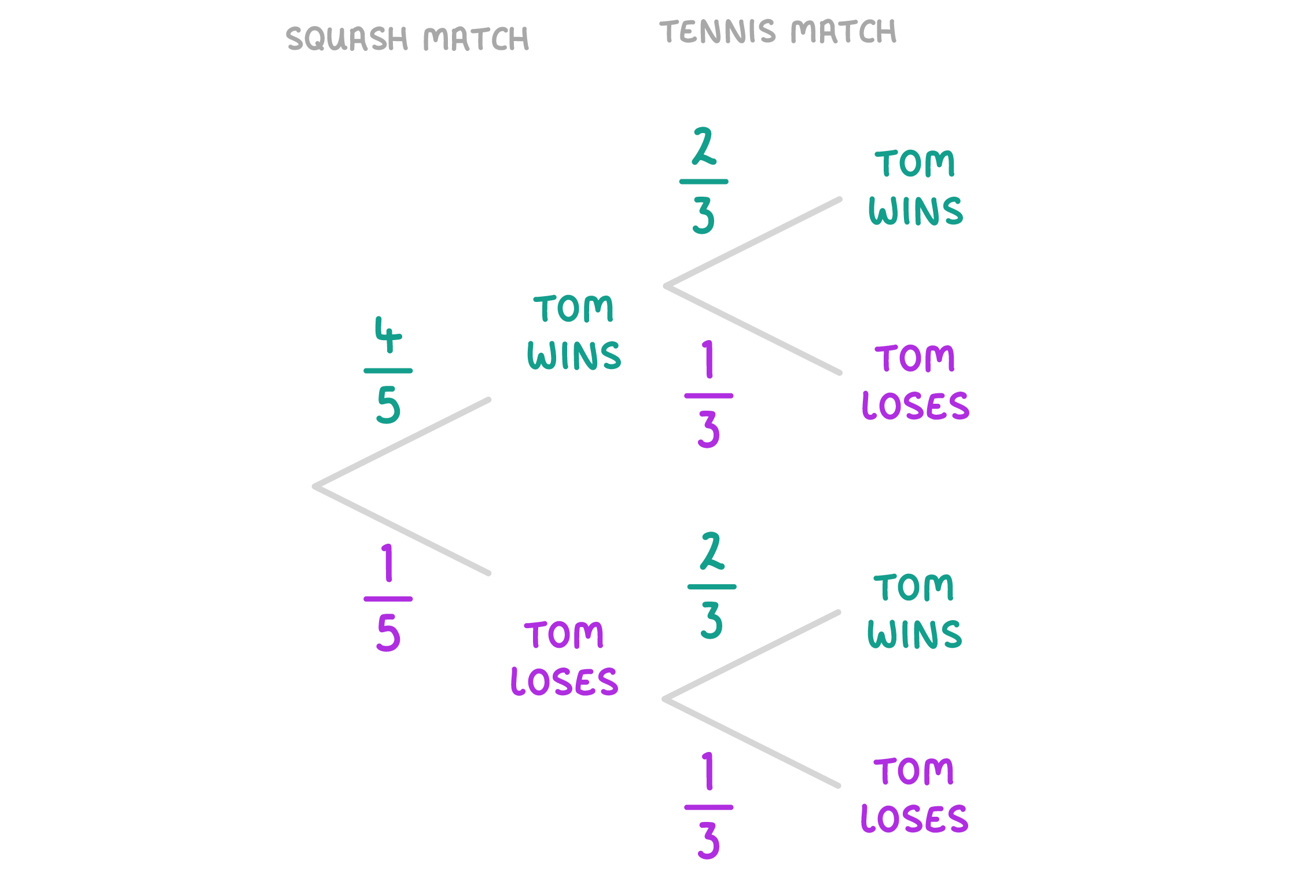

Probability tree diagram showing outcomes for Tom's squash and tennis matches with probabilities of winning and losing.

Part 2: Use the AND rule.


From the tree diagram, we can see that there are two paths in which tom only wins one game:

  1. He wins squash, but then loses badminton
  2. He loses squash, but then wins badminton


We can find the probability of each of these paths using the AND rule.

  1. P(win squash and lose badminton) = P(win squash) x P(lose badminton) = 4/5 x 1/3 = 4/15
  2. P(lose squash and win badminton) = P(lose squash) x P(win badminton) = 1/5 x 2/3 = 2/15


Part 3: Use the OR rule.


The final step is to add the two probabilities we've found together, to find the probability of either of them happening. 


P(winning only one game) = 4/15 + 2/15 = 6/15

P(winning only one game) = 2/5 (this is 6/15 simplified)

Using the tree diagram below, what is the probability that Tom wins both the squash match and the badminton match? 


Give you answer as a fraction in its simplest form. 


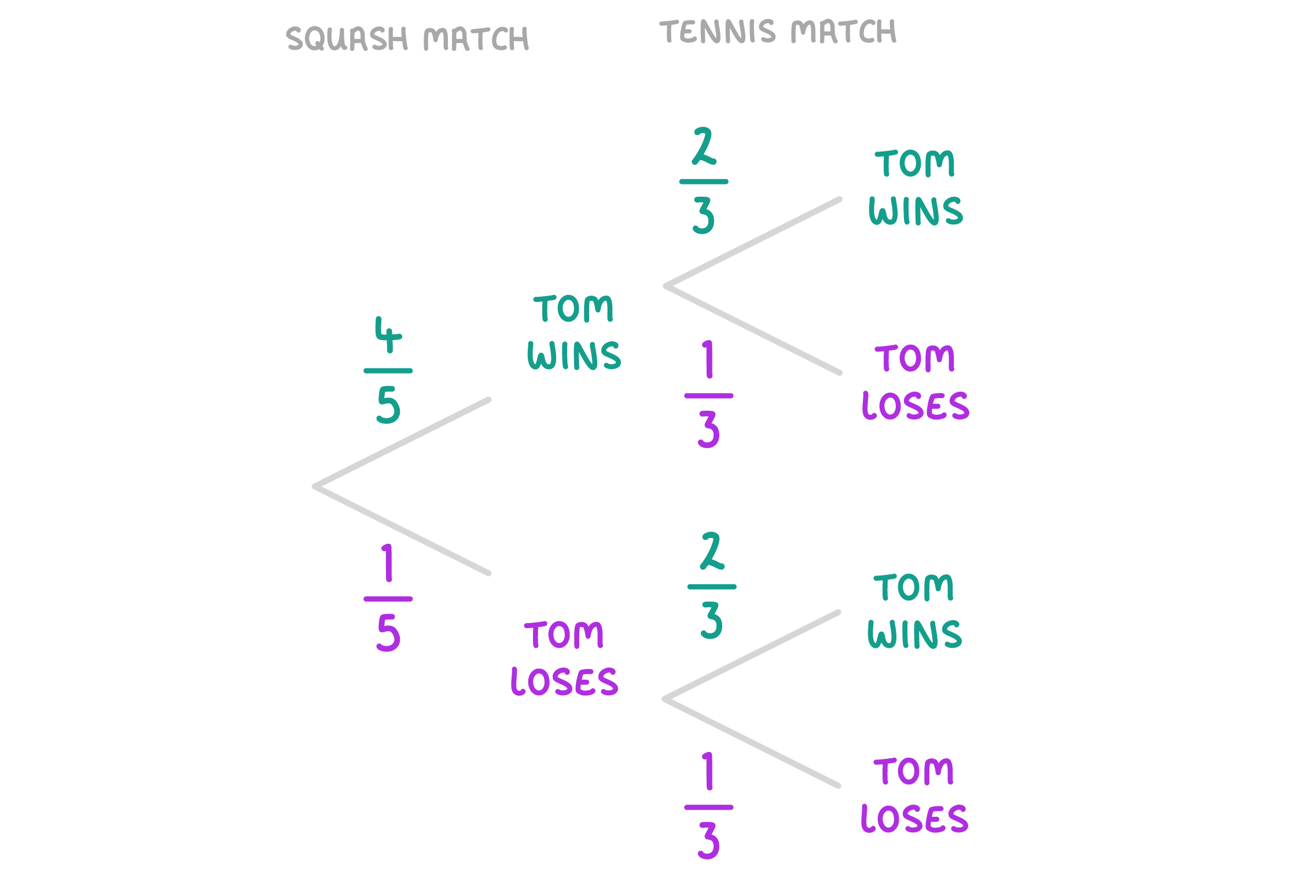
Tree diagram showing the probability of Tom winning both the squash match and the tennis match.
\frac{8}{15}

0

/

1

Using the tree diagram below, what is the probability that Tom loses both the squash match and the badminton match? 


Give you answer as a fraction in its simplest form. 


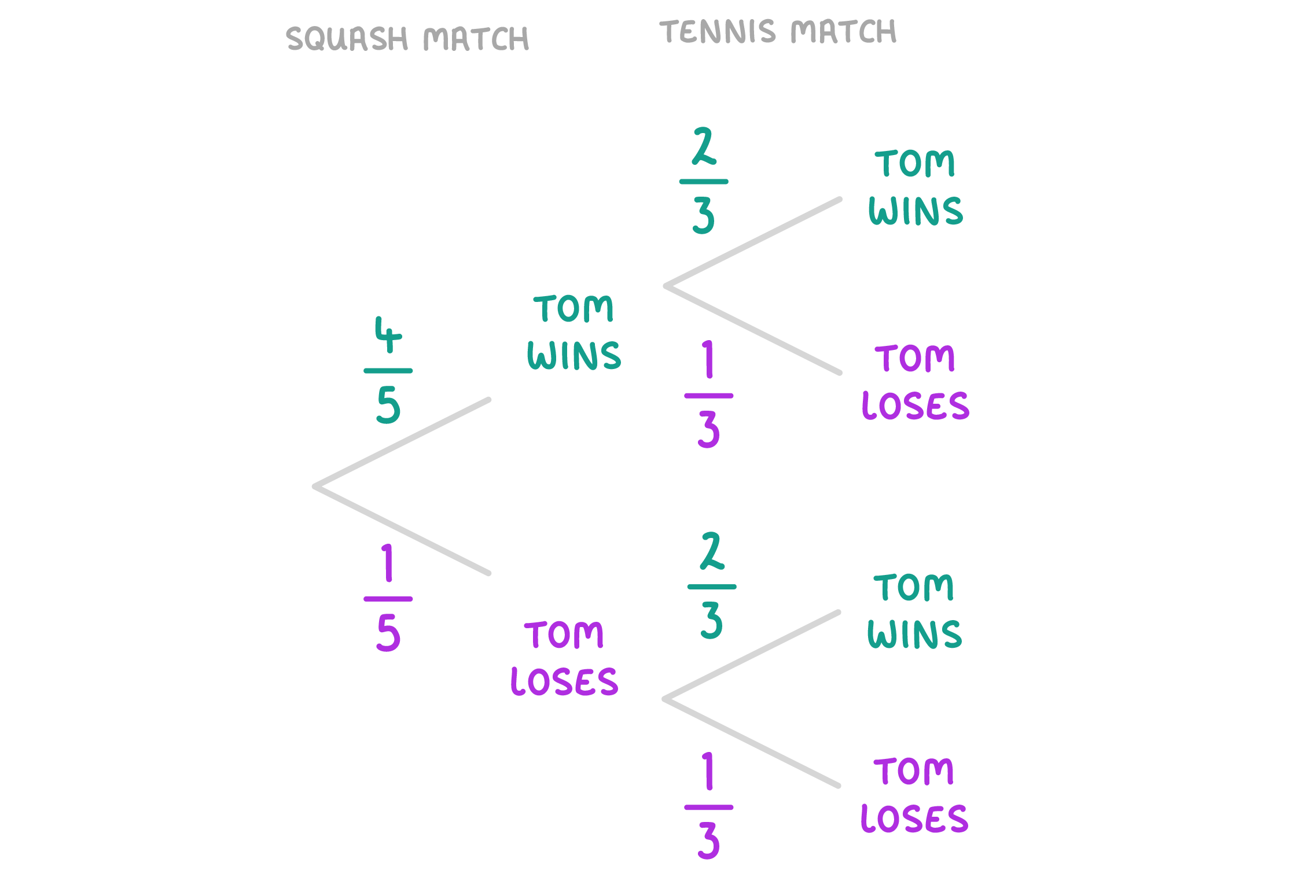
Tree diagram showing probabilities of Tom winning or losing squash and badminton matches.
\frac{1}{15}

0

/

1

The diagram below shows the first branch of a probability tree. 


What should the missing probability be?

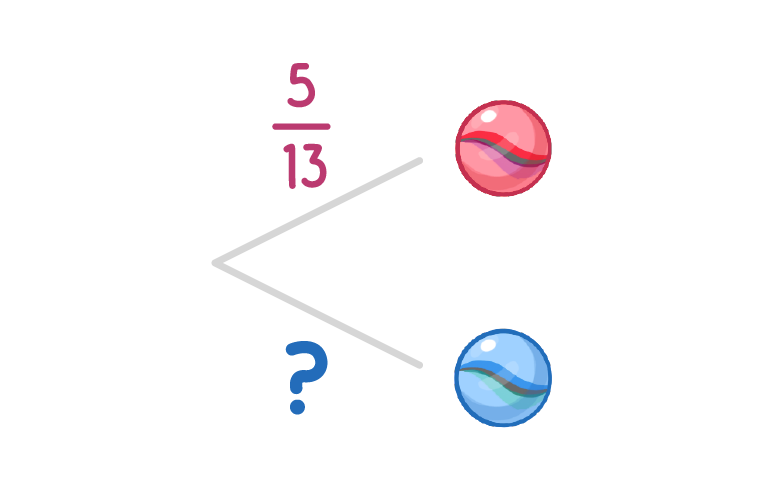
Diagram showing the first branch of a probability tree with a missing probability.
\frac{8}{13}

0

/

1

The image below shows a probability tree for picking 2 marbles from a jar. The first marble is replaced before picking the second.


What is the missing probability?

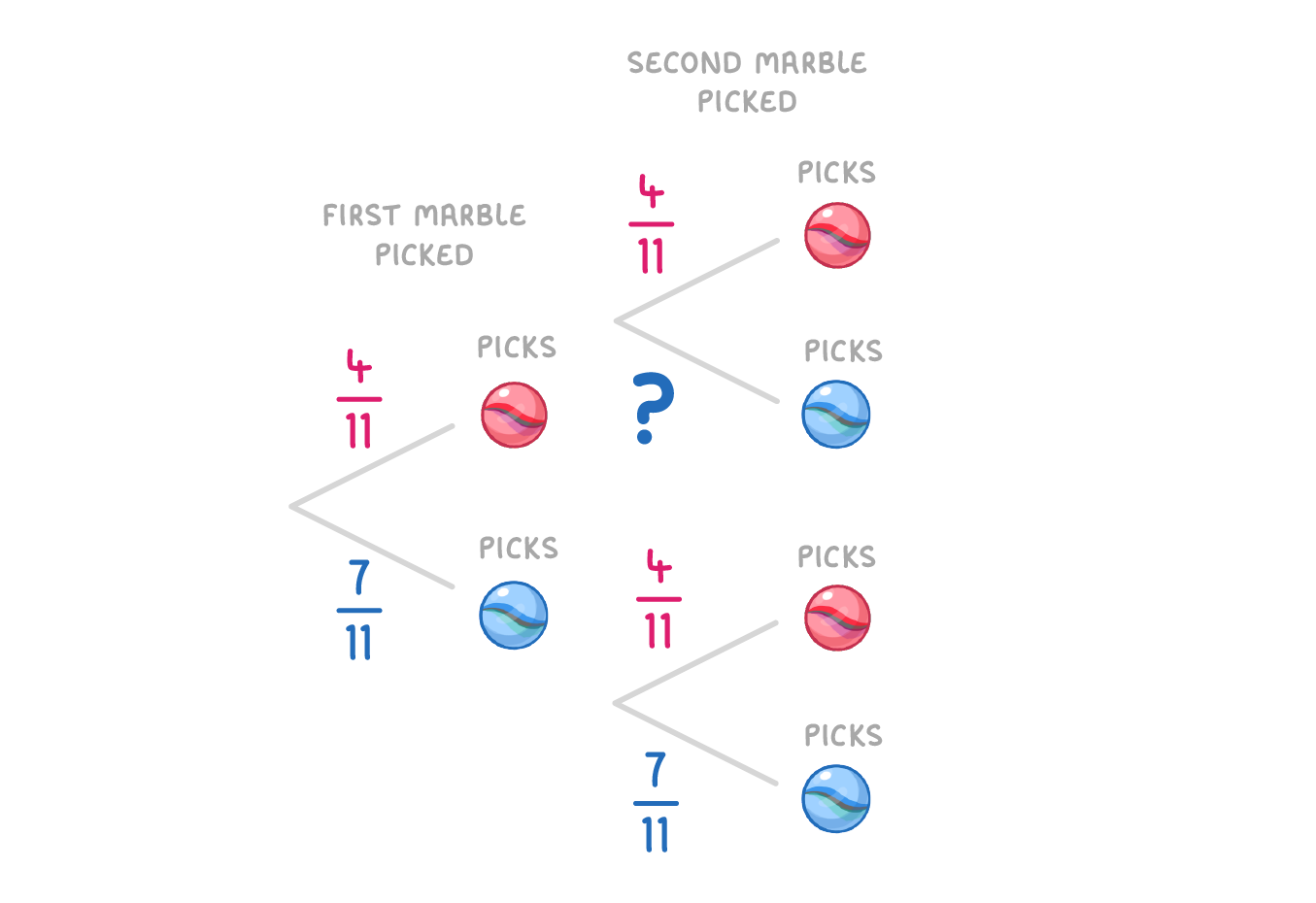
Probability tree diagram showing the chances of picking red or blue marbles from a jar with replacement.
\frac{7}{11}

0

/

1

The image below shows a probability tree for picking 2 marbles from a jar. The first marble is replaced before picking the second.


What is the probability of both marbles being blue? Give your answer as a fraction in its simplest form.

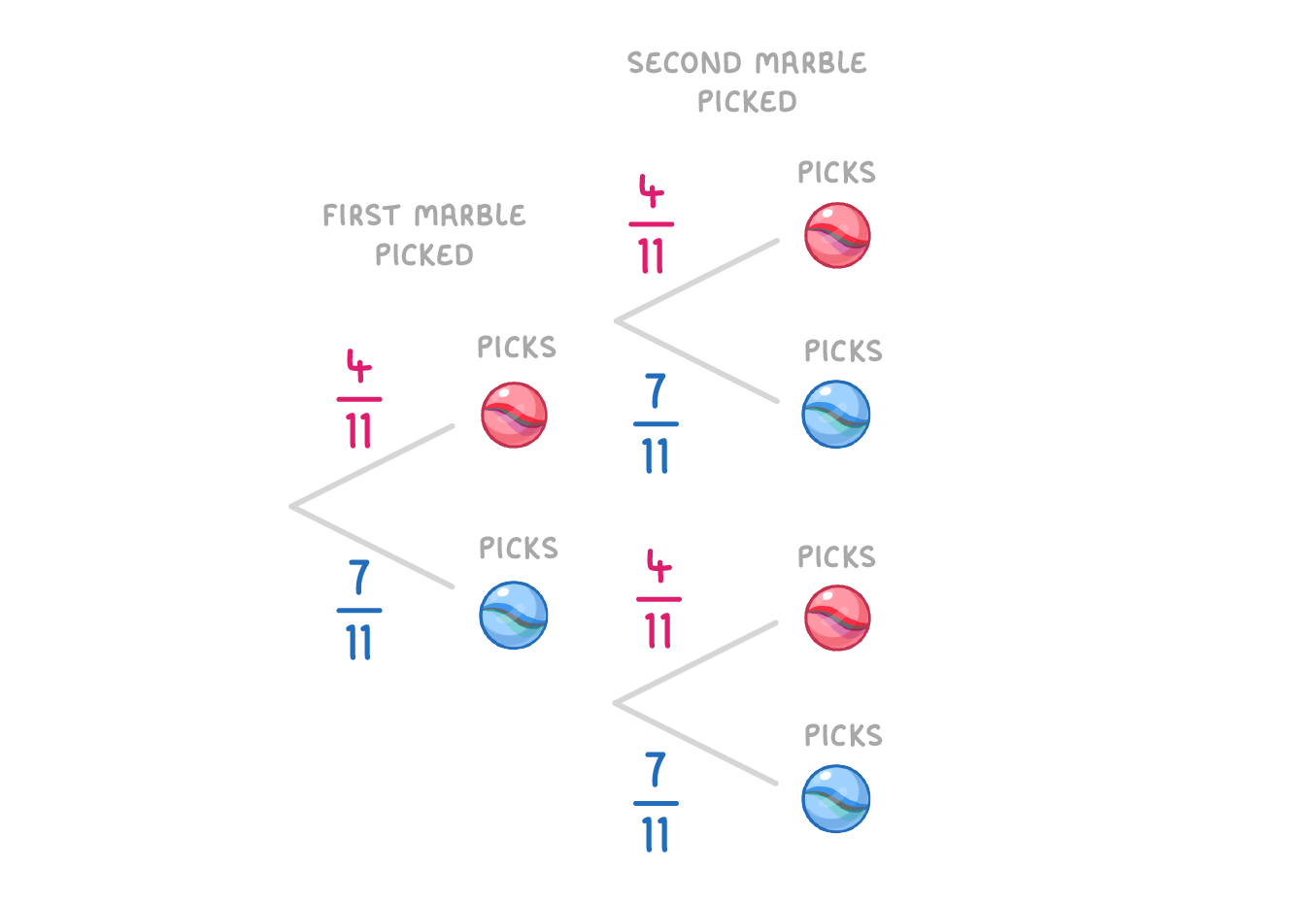
Probability tree diagram showing the chances of picking two marbles from a jar with replacement.
\frac{49}{121}

0

/

1