Probability Basics
This lesson covers:
- What probability is
- The concept that probability values are between 0 and 1
- How to find the probability of an outcome
- The idea that the probabilities of all possible outcomes add up to 1
What is probability? Probability is simply how likely something is to happen. The probability of an event can range from being impossible, all the way to being certain. |
 We can express probabilities on a scale like the one above. Probabilities can be expressed as a decimal (0.25), a fraction (1/4), a percentage (25%), or in words ('unlikely'). |
Which of the following is not a measure of probability?
Percentage
Decimal
Ratio
Fraction
|
What is the probability of getting heads when you flip a coin?
0.5
0
0.75
0.25
1
|
What is the probability of landing on 4 when you roll a fair dice?
|
Probability Notation To express the probability of something happening mathematically, we write P(something). You will often see the something represented with an X, so you might see 'the probability of X as P(X)'. |
 For example, if the probability that it will rain today is 80%, or 0.8, then we would write: P(Rain) = 0.8. |
What is the correct mathematical notation for showing that the probability of 'X' happening is 40%?
pX = 0.4
P of X = 0.4
P(X) = 0.4
|
What is the correct mathematical notation for showing that the probability of 'X' happening is 25%?
|
Probabilities add up to 1 If you consider all possible outcomes of an event, then all the probabilities must add up to 1. For example, if you flip a coin, the probability of it landing on heads and the probability of it landing on tails must add up to 1, because heads or tails are the only possible outcomes when you flip a coin. |
You may sometimes see this idea expressed as: P(event happens) + P(event doesn't happen) = 1 (be aware this only holds true if only one outcome can occur at a time. E.g. flipping a coin, which can only be heads or tails, it can't be both at once - or rolling a dice, which can only land on one number at a time) |
The probability of Carl completing his homework on time is 70%.
What is the percentage probability that he will not complete it on time?
%
|
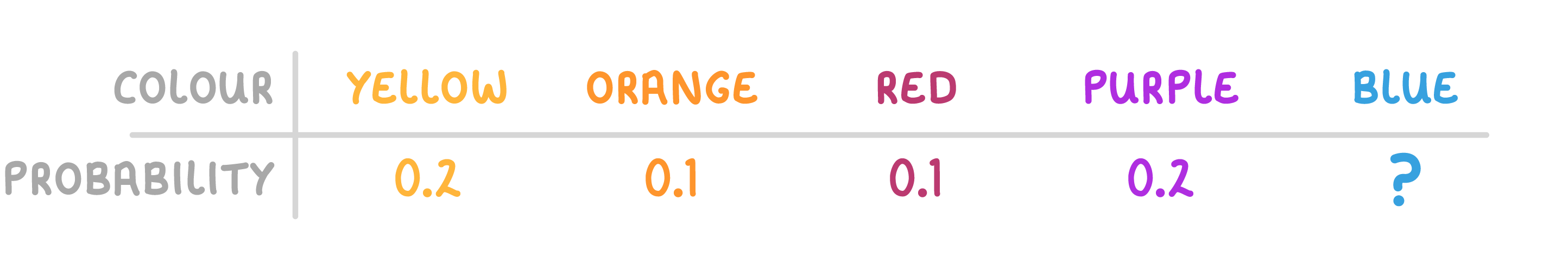
A bag contains yellow, orange, red, purple, and blue sweets. The probability of picking each colour is shown in the table above.
What is the probability of picking a blue sweet? Give your answer as a decimal.
|
How to calculate probabilities To calculate the probability when all possible outcomes are equally likely, we can use the following formula: probability = total number of possible outcomesnumber of ways an outcome can happen |
Example: What is the probability of rolling a 3 on a fair six-sided die?
|
So our formula becomes: probability = total number of possible outcomes number of ways an outcome can happen = 61 |
So the chance of rolling a 3 is 1/6. We could also express this as 16.7%, or 0.167. (you could also say it is 'unlikely', but in maths you should express probabilities as numbers whenever possible) |
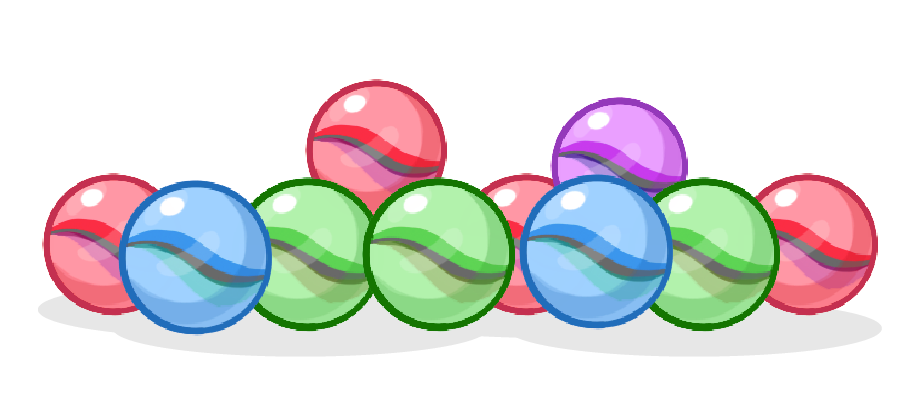
A bag contains 10 marbles. 3 of those marbles are green.
What is the probability of picking a green marble from the bag?
7/10
1
0
3/10
|
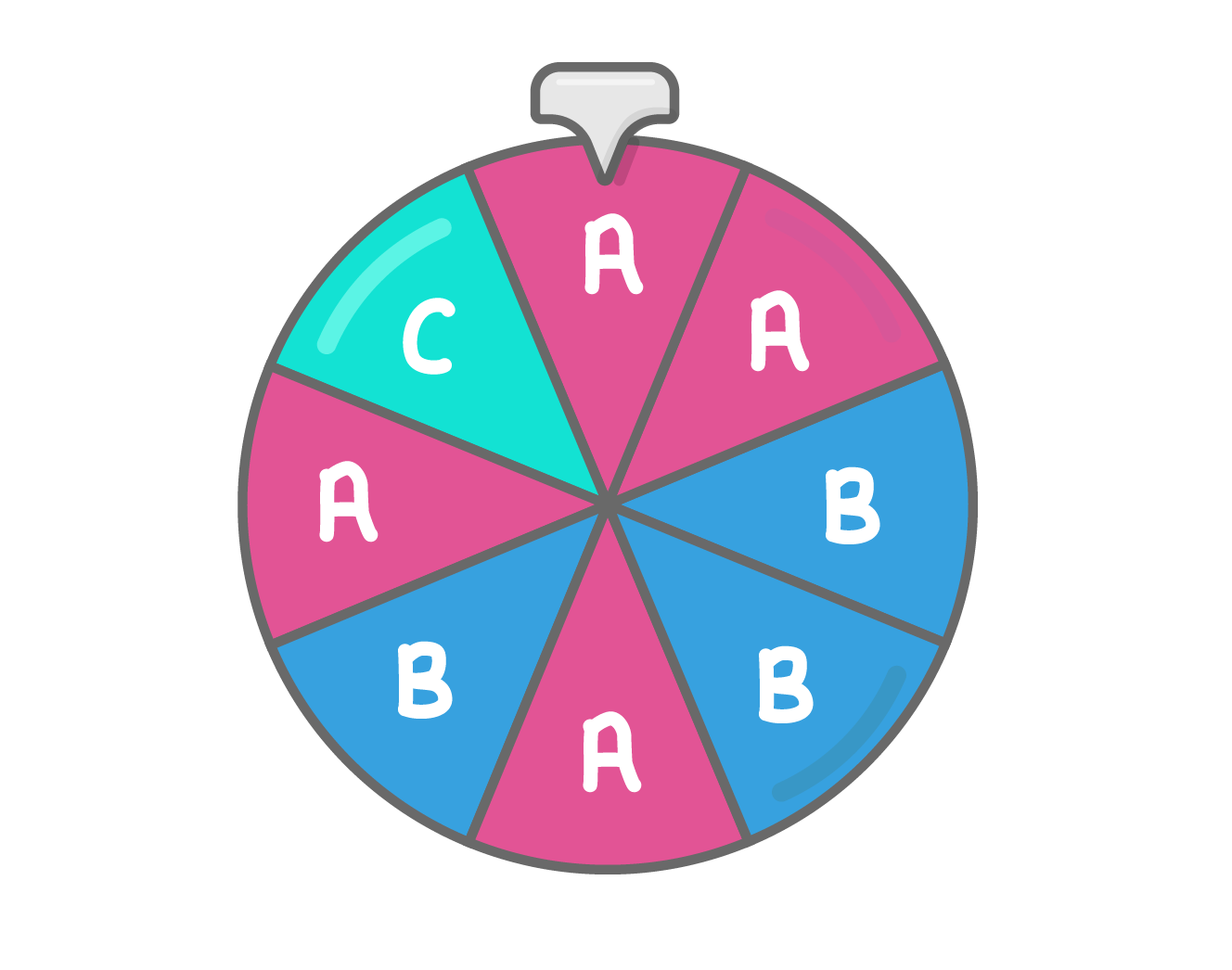
The diagram below shows a fair, 8-sided spinner. The spinner can land on A, B, or C.
What is the probability of the spinner landing on A?
3/8
1/2
1/4
1/8
|