Differentiation

This lesson covers: 

  1. How to differentiate a function
  2. Differentiation using the gradient of a graph
  3. How to find the location of stationary points on a graph

Differentiation of a function


Differentiation is a method to find the rate of change of a variable.

The differentiated function is called the derivative, represented as dxdy​.  


Consider the function below:

y = kxn


When we differentiate the function it becomes:


dxdy​= nkxn−1


To differentiate, multiply each variable by the power and subtract 1 from the power.


Special cases:

  • kx differentiates to become k.

Example - 4x differentiates to become 4.


  • A number on its own will become zero when differentiated.

Example - 6 differentiates to become 0.

Worked example 1: Differentiation of a function

Differentiate the function y = 3x4.

Worked example 2: Differentiation of a function

Differentiate the function y = 4x.

Worked example 3: Differentiation of a function

Differentiate the function y = 7.

Worked example 4: Differentiation of a function

Differentiate the function y = 2x3 + 4.

Worked example 5: Differentiation of a function

Differentiate the function y = 3x2 + 4x - 5.

Worked example 6: Differentiation of a function

Differentiate the function y = 3x4 - 6x + 3.

Differentiate the function y = 6x2 + 4x - 10.

dxdy​=10x
dxdy​=12x2−4
dxdy​=6x+4
dxdy​=12x+4

0

/

1

Differentiate the function y = 4x3+2x+7

dxdy​=6x+2
dxdy​=12x+2
dxdy​=12x
dxdy​=12x2+2

0

/

1

Differentiate the function y =−5x2+6x−3

dxdy​=−10x+6
dxdy​=−10x−6
dxdy​=10x2+6
dxdy​=10x+6

0

/

1

Differentiate the function y=−2x3+4x−8

dxdy​=3x2+4
dxdy​=8x+4
dxdy​=−6x2+4
dxdy​=−4x−8

0

/

1

Differentiating a graph gives the gradient


Consider a line with the equation y = 2x + 3.

Differentiating this equation gives dxdy​=2.


We can also find the derivative by finding the gradient of the graph:

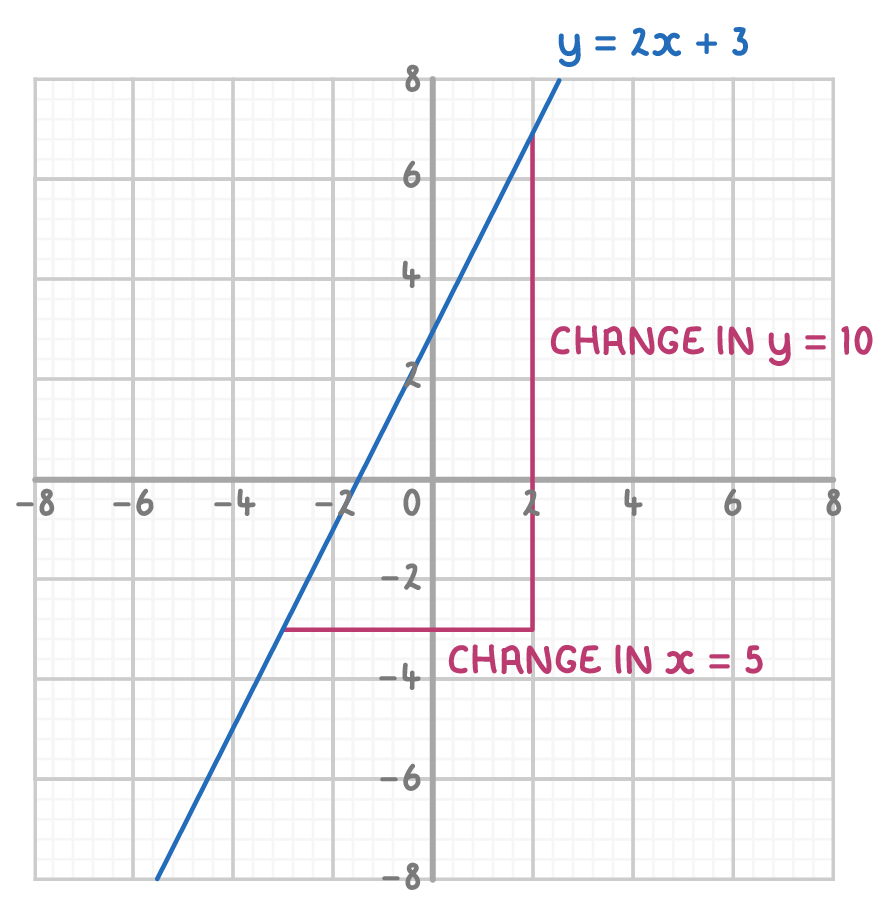
Graph showing the line y equals 2x plus 3 with gradient calculation

gradient = dxdy​=runrise​=change in xchange in y​


dxdy​=510​=2

Stationary points


A stationary point is where the gradient = 0. 


There are two types of stationary points: 

  • Maximum point - the point where the y coordinate has the highest value.
  • Minimum point - the point where the y coordinate has the lowest value.
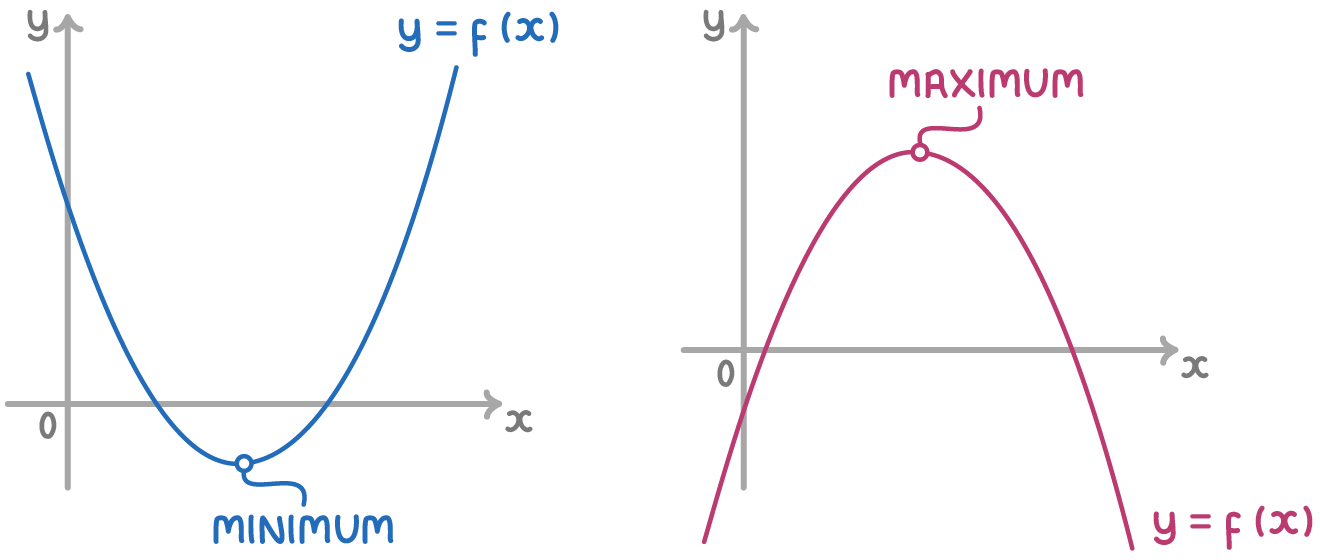
Graph showing minimum and maximum stationary points on a curve.

What type of stationary point is shown in the diagram?

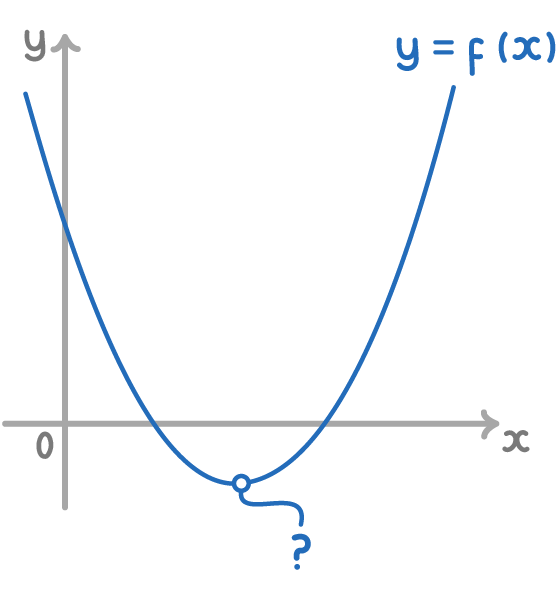
Graph showing a stationary point on a curve y equals f of x with a question mark indicating the type of stationary point.

Minimum

Maximum

0

/

1

Worked example 1: Finding the location of stationary points


Consider the curve y = 2x2 - 4x - 5


The location of the stationary point occurs when the gradient = 0

Worked example 2: Finding the location of stationary points


Consider the curve y = 3x2 + 2x + 4


The location of the stationary point occurs when the gradient = 0

Identify the coordinates of the stationary point of the curve.

y =3x2−12x+2

(-2, 10)

(2, 4)

(4, -2)

(2, -10)

0

/

1