Conditional Probability

This lesson covers:

  1. What conditional probability means
  2. How to do calculations involving conditional probability

Conditional probability


Conditional probability is the probability of an event happening given that another event has already happened.


You might see this expressed as 'the conditional probability of B given A' - which just means 'the probability that event B happens, if event A happens'.

Conditional probability only applies to dependent events. The formula to remember is:


P(A and B) = P(A) x P(B given A)

Example: 


Tom plays tag rugby on the weekends. The probability that he is in the starting lineup is 0.8.

If he starts the game, the probability that he scores a try is 0.7.


What is the probability that Tom is in the starting lineup, but does not score a try?


Step 1: Think about what we're trying to find.


We want to find the probability that Tom starts AND doesn't score, or P(starts and doesn't score)

let's say 'starts' is event A and 'doesn't score' is event B.


So we're trying to find: P(A and B).


Step 2: Write the formula.


P(A and B) = P(A) x P(B given A)


Step 3: Find P(A) and P(B given A).


P(A) is the probability that he starts, which we're told is 0.8.


P(B given A) is the probability that he doesn't score, given that he starts.

  1. We're told that the probability that he does score, given that he starts is 0.7.
  2. So to find the probability that he doesn't score, given that he starts, we do 1 - 0.7 = 0.3. 


Step 4: Plug the values into the formula


P(A and B) = P(A) x P(B given A)

P(A and B) = 0.8 x 0.3 = 0.24

Conditional probability trees


When we represent dependent events on a probability tree, the probabilities will change as you go along the tree, depending on the previous event.


Example:

A bag contains 3 blue marbles and 5 green marbles.


Diya picks 2 marbles at random without replacing them. Draw a probability tree and calculate the probability that she selects two blue marbles.

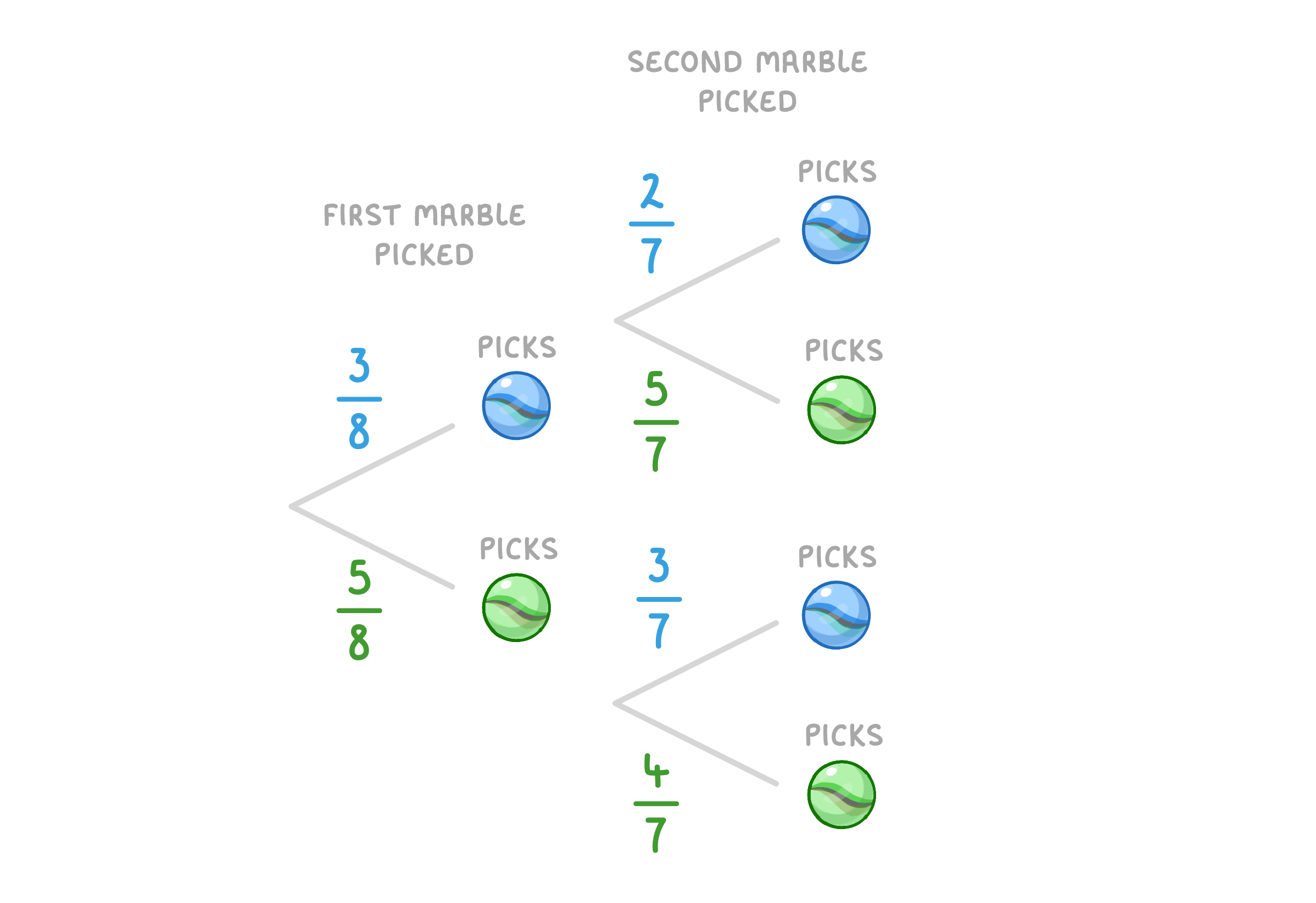Diagram showing a conditional probability tree for picking blue and green marbles without replacement.

There are 8 marbles in total to begin with, so for the 1st marble the probability of picking a blue one is 3/8, and the probability of picking a green one is 5/8,

However, for the 2nd pick, the number of marbles will have changed, so the probabilities will have changed. For example, if she picked a blue marble the 1st time, then the probability of picking blue for the 2nd pick will change to 2/7, as there are only 2 blue marbles left out of a total of 7. 

Step 2: Find the relevant branch route(s).


To pick two blues marbles she must pick a blue in the 1st pick, and then blue again for the 2nd pick.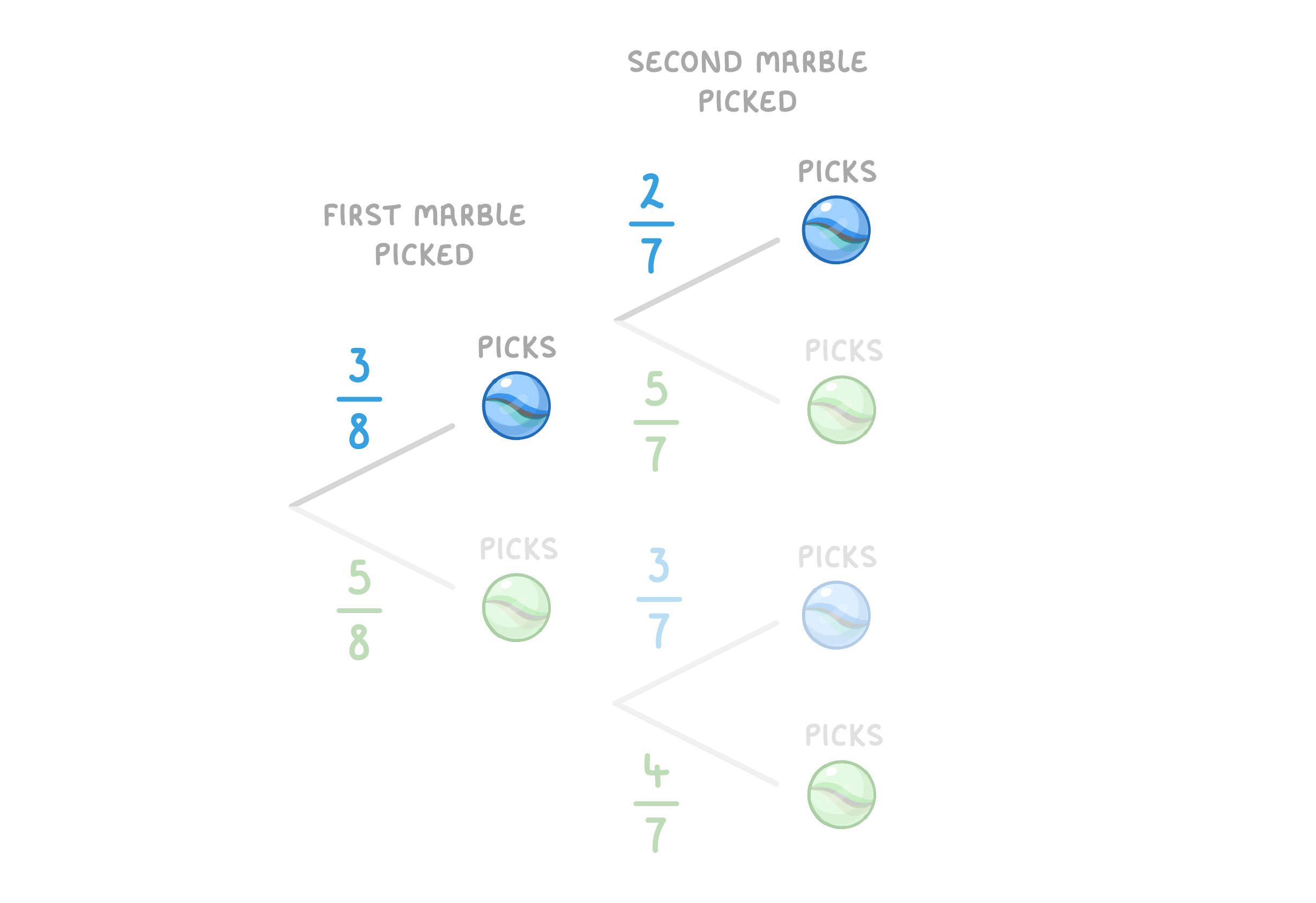

Conditional probability tree diagram showing probabilities of picking blue and green marbles.

Step 3: Calculate the probability.


P(blue and blue) = 3/8 x 2/7 = 6/56 = 3/28 (simplified)


P(blue and blue) = 3/28

A bag contains 6 blue marbles and 4 purple marbles. Sam picks a random marble out of the bag. They don't replace the marble after taking it out.


They then take a second random marble from the bag.


Draw a tree diagram to show the probability of each possible outcome.


(press 'Continue' to check your answer)

[0/3]

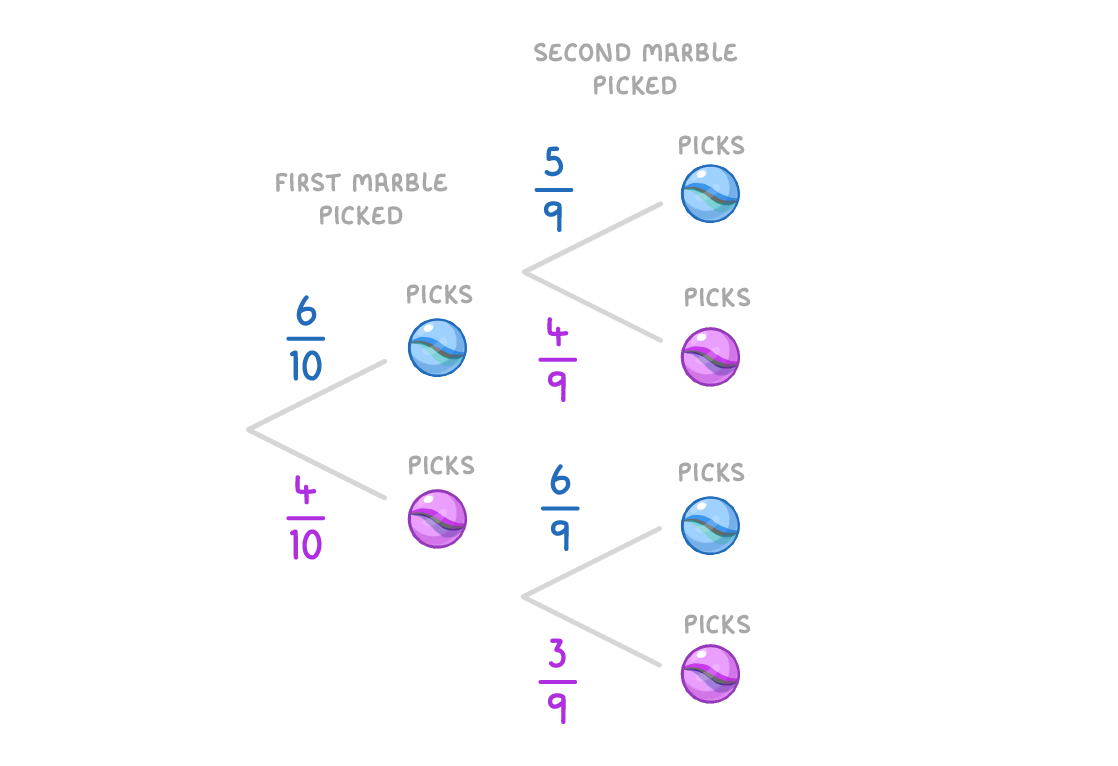Tree diagram showing the probabilities of picking two marbles of the same or different colours from a bag without replacement.

Work out the probability that both the marbles Sam picks are the same colour.

\frac{7}{15}|\frac{42}{90}|\frac{14}{30}\frac{21}{45}

[0/1]

0

/

4