Terms to know

A sample space refers to all the possible outcomes of an experiment.

A sample space diagram is a table showing all the possible outcomes (a table of the sample space).

Listing all outcomes means making a list of all the possible outcomes (a list of the sample space).

For example, when rolling a die, the possible outcomes are 1, 2, 3, 4, 5, or 6.

Counting all outcomes means counting how many possible outcomes there are. In this case, you don't need to list what they are, just how many of them there are. 

For example, when rolling a regular die, there are six possible outcomes. 

The product rule is a technique for finding the total number of outcomes.

It states that the total number of outcomes for two or more events is equal to the number of outcomes for each event multiplied together.

Sample space diagrams

A sample space diagram is a table showing all the possible outcomes of an experiment. We tend to use sample space diagrams when we combine the outcomes of multiple events.

For example, the below sample space diagram shows the all possible outcomes when rolling two six-sided dice, and adding up their scores.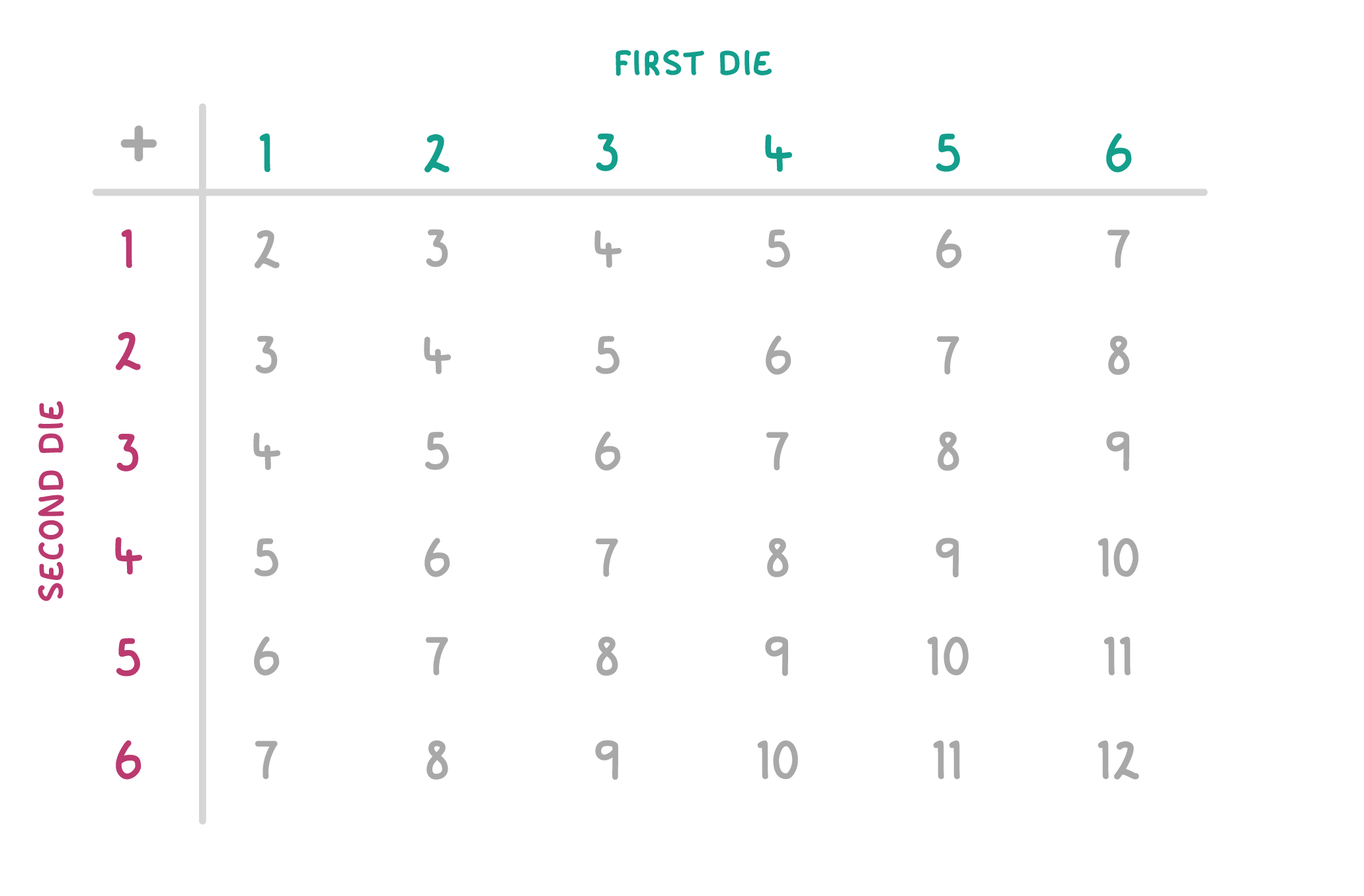

Example:

Nima rolls two fair six-sided dice. What is the probability that both dice add up to 8?

Step 1: Draw out a sample space diagram, and count the number of outcomes where the added total is 8. In this question that will be 5.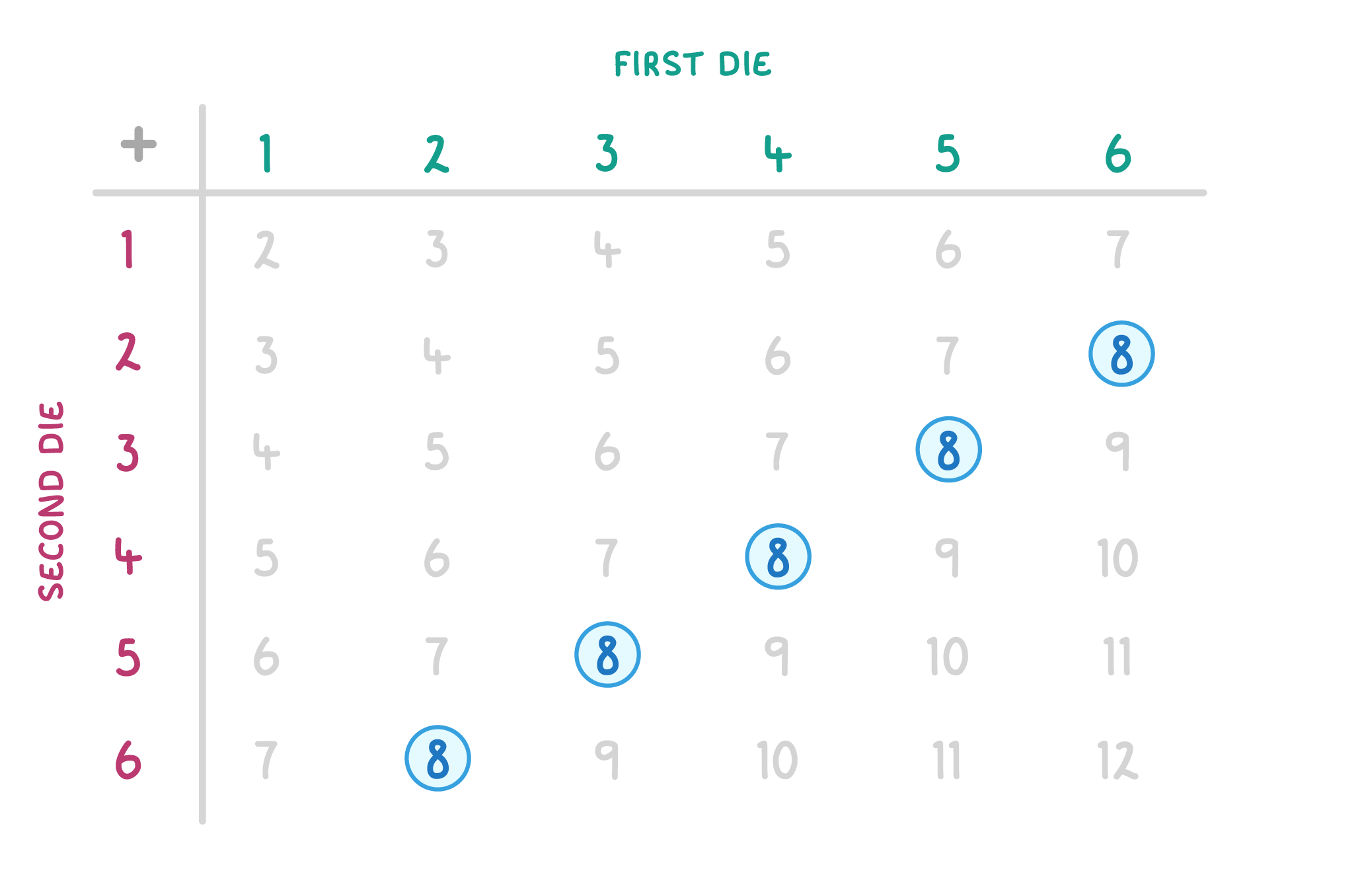

Step 2: Work out the number of possible outcomes.

Do this by multiplying together the number of possible outcomes for each variable:

no. of possible outcomes for first die x no. of possible outcomes for second die

Remember each die has 6 possible outcomes (1, 2, 3, 4, 5, 6) - so we do:

6 x 6 = 36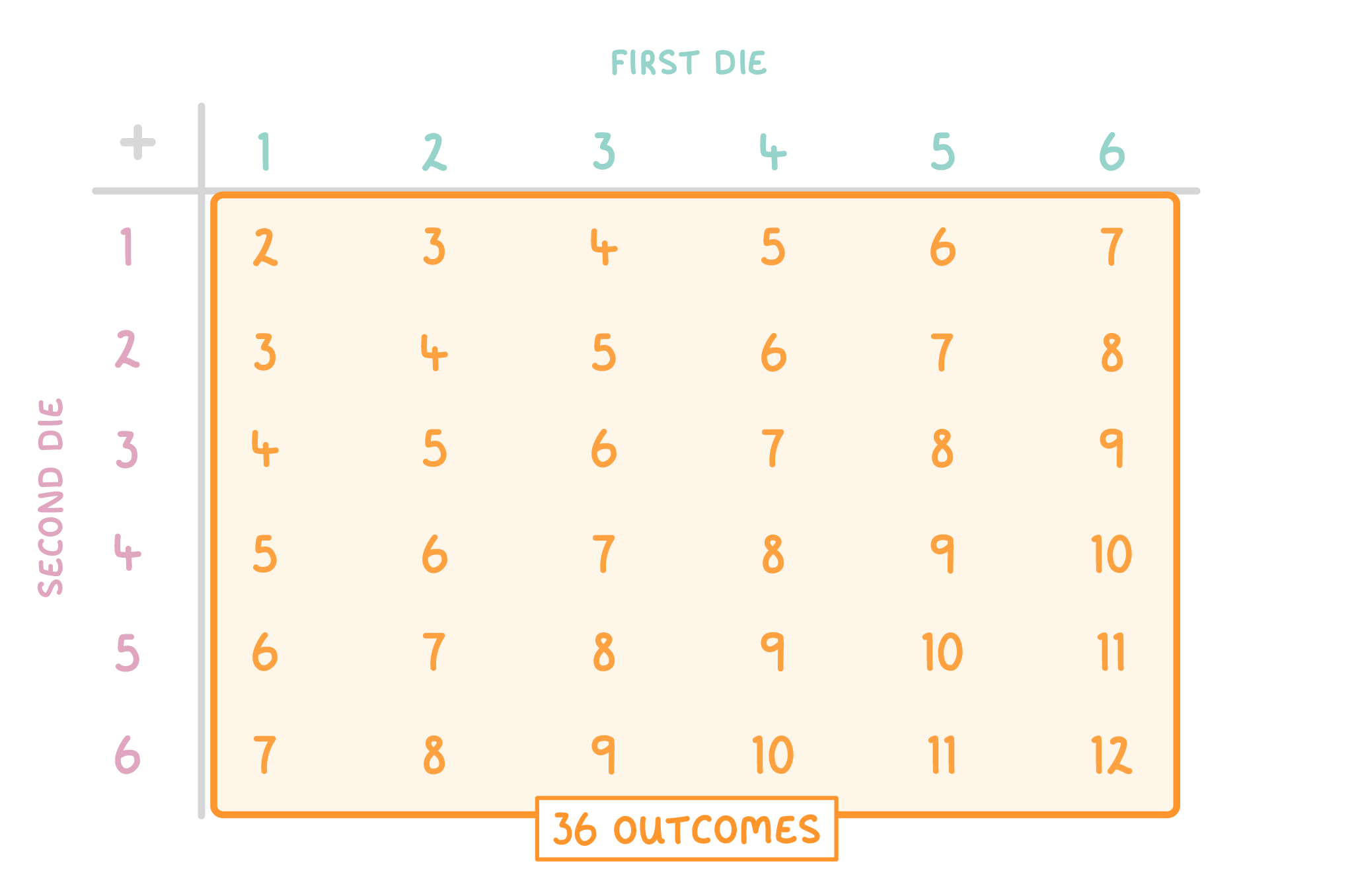

Step 3: Use the values you just found to calculate the probability that both dice add up to 8:

Product rule

If there are a large number of outcomes, or multiple events occurring - we can use the product rule to count the total number of outcomes (we could list all the possible outcomes if we wanted to, but this will often take a long time).

The product rule states:

The total number of outcomes for 2 or more events is equal to the number of outcomes for each event multiplied together.

Example:

Charlie has 2 pairs of shoes, 3 pairs of trousers, and 5 t-shirts. How many different outfits does he have to choose from?

To work this out, all we need to do is apply the product rule and multiply the number of options together:

number of different outfits = 2 pairs of shoes x 3 trousers x 5 t-shirts = 30

or

number of different outfits = 2 x 3 x 5 = 30