Vectors - Finding Unknown Lengths

This lesson covers: 

  1. How to find the magnitude of a vector
  2. How to find the vector of an unknown length

The magnitude of a vector


The magnitude of a vector tells us the size or length of the vector.

The length of a vector can be found using Pythagoras' theorem.

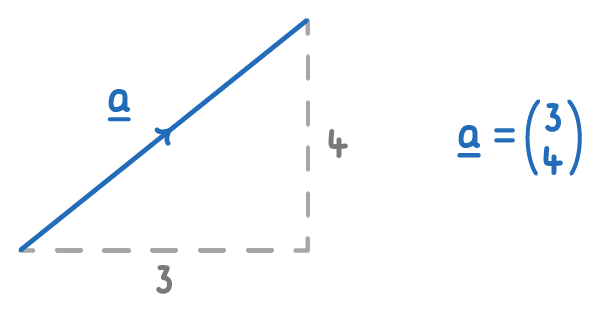
Diagram showing the calculation of the magnitude of vector a using Pythagoras' theorem with components 3 and 4.

The length of a​ is also known as the magnitude or modulus. This is represented as ∣a​∣.


∣a​∣=√32+42​=5

OAB is a triangle. 

OA = 2a and OB = 3b

Find AB in terms of a and b.

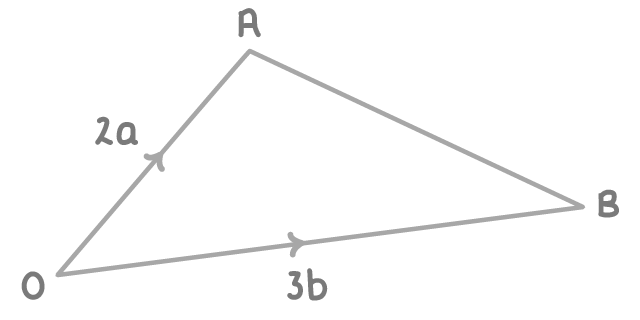
Triangle OAB with vectors OA equals 2a and OB equals 3b.

2a - 3b

3b - 2a

2a + 3b

-2a - 3b

0

/

1

Calculate the magnitude of the vector:

a = (15​)

26.00

2.50

6.00

5.10

0

/

1

Calculate the magnitude of the vector:

a = (−312​)

2.23

13.00

5.00

3.61

0

/

1

Calculate the magnitude of the vector:

a = (64​)

10.00

52.00

3.16

7.21

0

/

1

Worked example 1: Finding unknown lengths


We can use vectors to help find an unknown length.

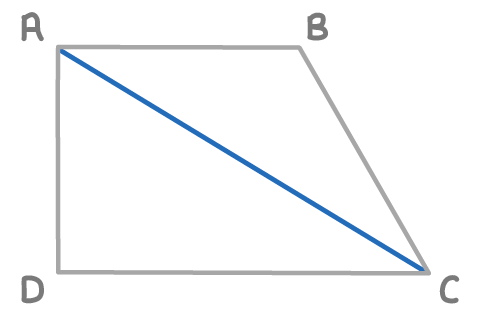
Diagram of a quadrilateral with vertices labeled A, B, C, and D, and a diagonal line AC.

Find the length AC, given the following vectors:

AB=(03​)    CD=(10−4​)   AD=(−310​)

Worked example 2: Finding unknown lengths


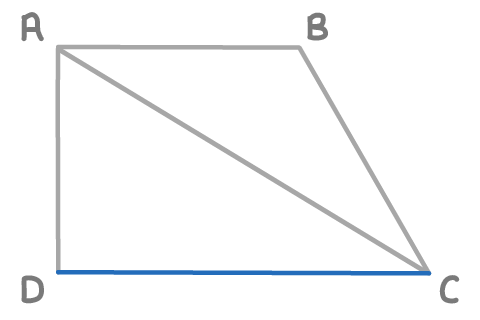
Find the length DC, given the following vectors:

AC=(−514​)    BC=(−511​)   AD=(−510​)

Diagram showing vectors and points A, B, C, and D for finding unknown lengths

Find the length AC, given the following vectors:

AB = (−412​)  CB = (73​)   DA = (31​)

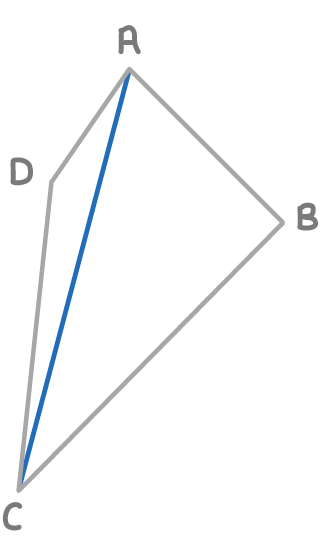
Diagram showing vectors AB, CB, and DA used to find the length AC

11.05

5.83

4.12

3.58

0

/

1

ABC is a triangle. 

Given that a = (48​) and b = (−616​), find the magnitude of the length CB.

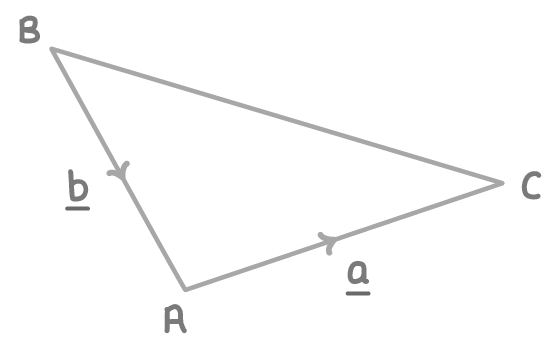
Diagram of triangle ABC with vectors a and b, showing how to find the magnitude of length CB.

-13.7

14.14

8.5

6.92

0

/

1