Vector Basics - Theory, Adding & Multiplying

This lesson covers: 

  1. What vectors are and how to represent them
  2. How vectors can be multiplied by scalars
  3. Adding and subtracting vectors

What are vectors?


Vectors are quantities that have both magnitude (size) and direction. Examples of vectors include velocity, displacement, and acceleration.

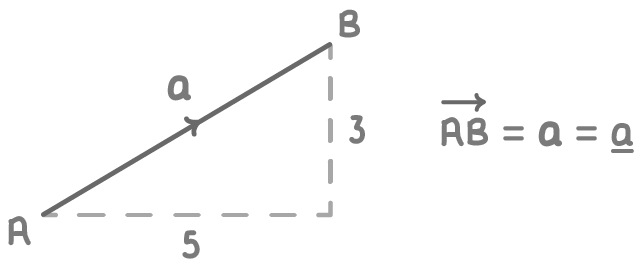
Diagram showing vector notation with a vector from point A to point B, represented as a column vector, bold notation, and arrow notation.

Vector notation:

  • Column vectors - Represented as vertical columns, such as (35​), indicating movement of 5 units right and 3 units up.
  • Bold notation - Used in textbooks and exams, represented by bold characters like a.
  • Arrow notation - Represented as AB , showing a vector going from point A to point B.
  • Underlined - Represented as a letter underlined, such as a.


Multiplying a vector by a scalar


When vectors are multiplied by scalars (numbers), the size of the vector changes, but its direction remains the same. 

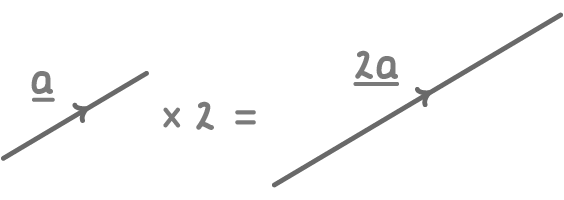
Diagram showing a vector a multiplied by a scalar 2 resulting in vector 2a.

Key points:

  • Positive scalars scale up the vector while keeping the direction the same.
  • Negative scalars reverse the direction of the vector.

Worked example 1: Multiplying a vector by a scalar


Multiply the vector a = (42​) by 3.  

Worked example 2: Multiplying a vector by a scalar


Multiply the vector b = (14​) by -5.  

Adding and subtracting vectors


Vectors can be combined through addition or subtractions to describe new resultant vectors.


Adding vectors:

To add vectors, align them tip to tail and the resulting vector runs from the tail of the first vector to the tip of the second. 

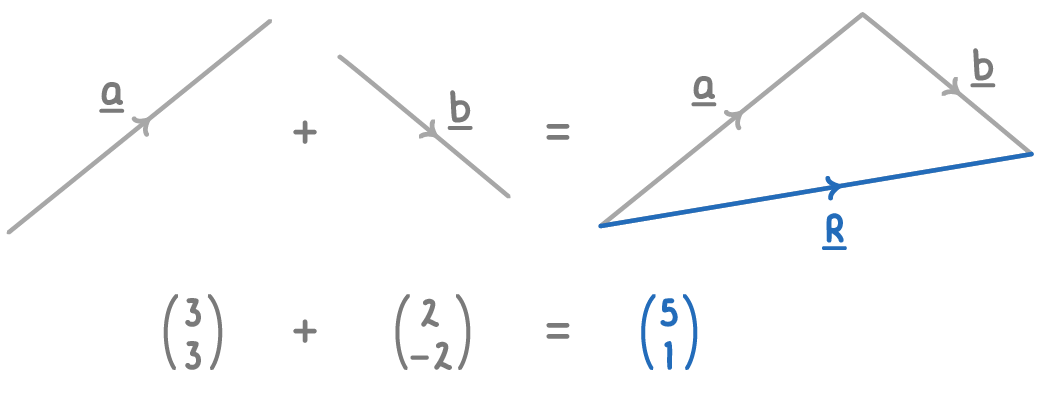
Diagram showing vector addition with vectors a and b resulting in vector R

Subtracting vectors:

Subtracting a vector is like adding its negative; it involves reversing the direction of the second vector before adding.

Diagram showing vector addition and subtraction with vectors a, b, and c.


a =(−215​)  c =(44​)


b = a - c


b =(−215​)−(44​)=(−611​)


Worked example 3: Vector addition.


Find the vector addition of a and b.

a =(52​)  b =(−6−3​)

Worked example 4: Vector addition.


Find the vector addition of a and b.

a =(36​)  b =(−214​)

Worked example 5: Vector subtraction


Find the vector subtraction of a - b.

a =(14−7​)  b =(−512​)

Find the value of 3a

a =(41​)  

(1213​)
(74​)
(13​)
(69​)

0

/

1

Find the value of 2a 

a =(12−3​)  

(13​)
(14−6​)
(46​)
(41​)

0

/

1

Find the value of b x -3 

b =(15−3​)  

(−151−9​)
(80​)
(−15119​)
(11−6​)

0

/

1

Find the value of a + b

a =(41​)  b =(12−6​)

(1615​)
(16−5​)
(69​)
(16−9​)

0

/

1