Similar Shapes
This lesson covers:
- What mathematically 'similar' shapes are
- How to use scale factors to find the lengths of missing sides on similar shapes
Which feature(s) must be identical for two shapes to be considered 'similar'?
Their shape
Their rotation
Their size
Their position
|
You can normally tell whether two shapes are similar just by looking at them. To be sure though, what would you need to confirm?
That all of the angles are the same size
That all of the sides are the same length, and all of the angles are the same size
That all of the sides are the same length
|
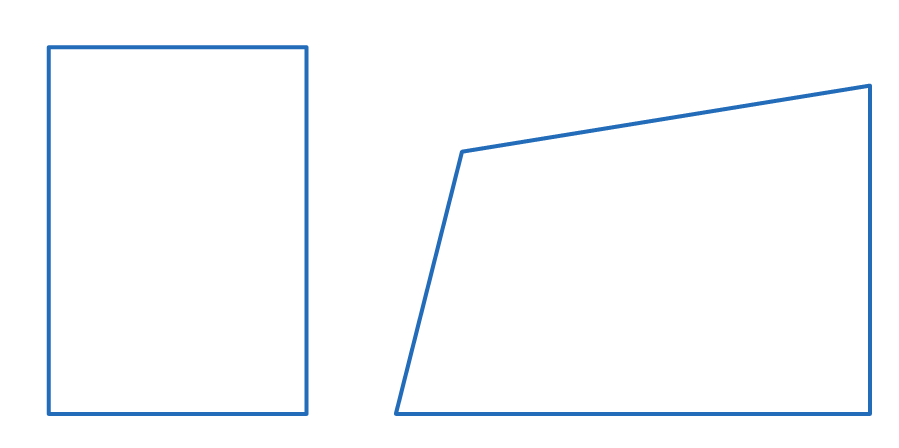
Are the above shapes similar?
Yes
No
|
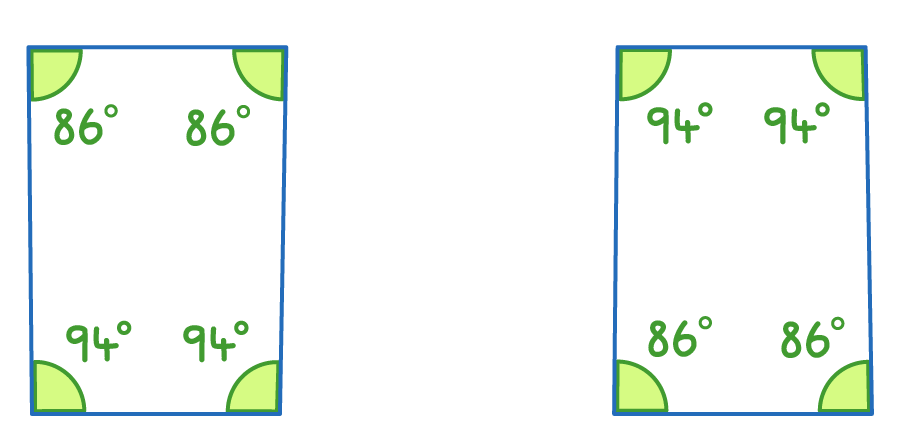
Are the above shapes similar?
No
Yes
|
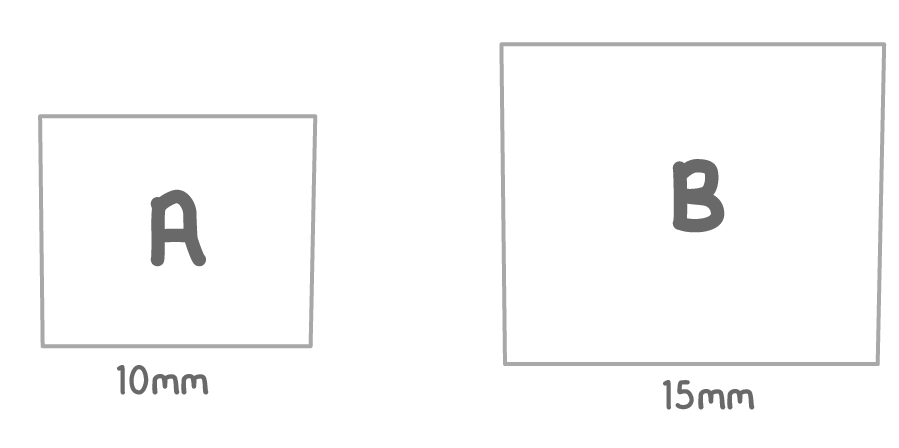
The two quadrilaterals above are similar. What is the scale factor from shape A to shape B?
|
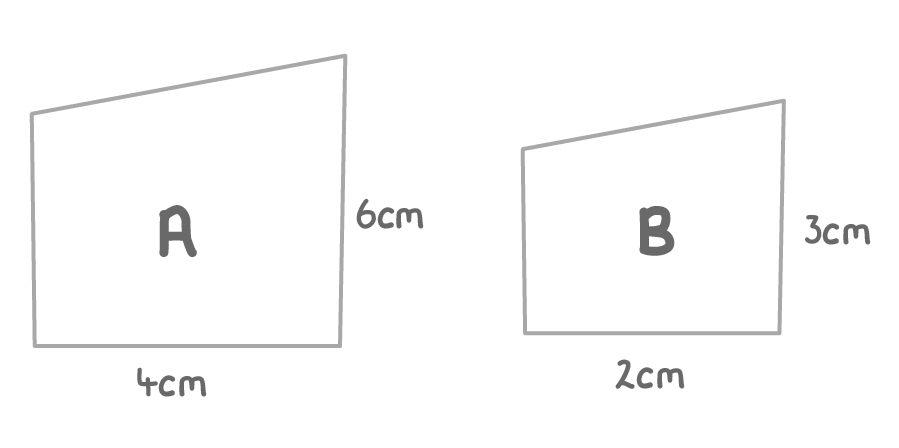
The two quadrilaterals above are similar. What is the scale factor from shape A to shape B?
|
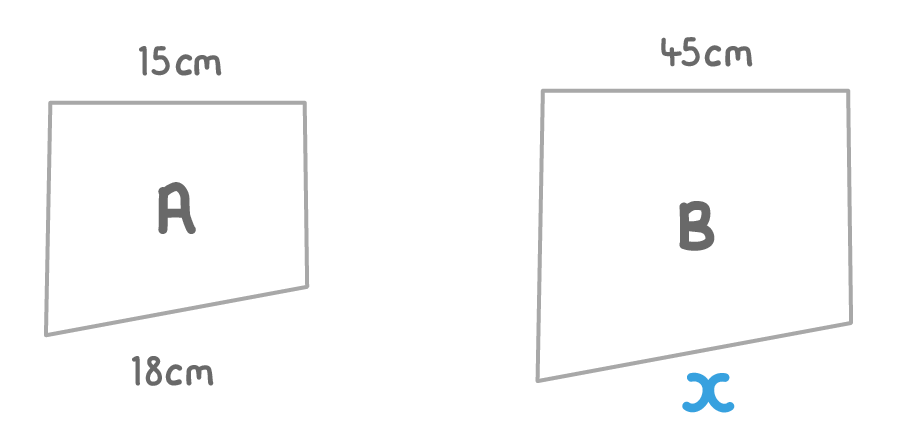
The two quadrilaterals above are similar. What length is side x?
cm
|
When discussing shapes, do the terms 'similar' and 'mathematically similar' mean the same thing?
Yes
No
|
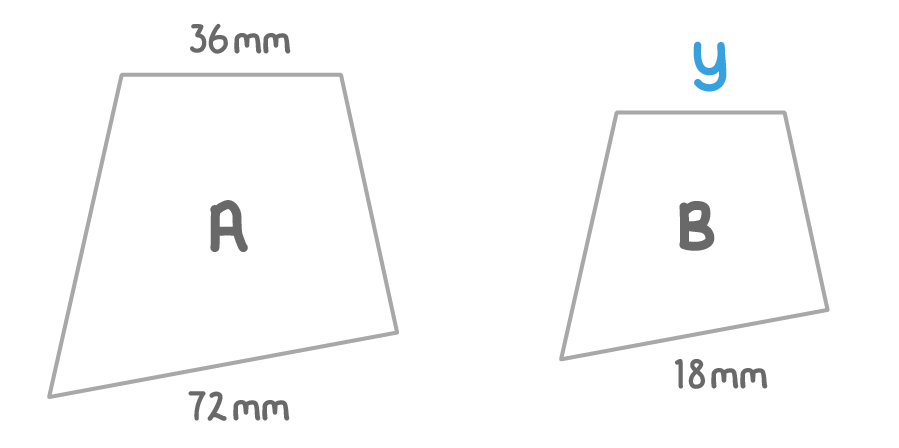
The two quadrilaterals above are similar. What length is side y?
mm
|