Using Ratios To Find A Point Along On A Line
This lesson covers:
- How to use ratios to find a particular point along a line
- E.g. 'ABC is a straight line. AB : QR is 2 : 5. Point A is at (-7, 5) an C is at (14, -2). Work out the coordinates of point B.'
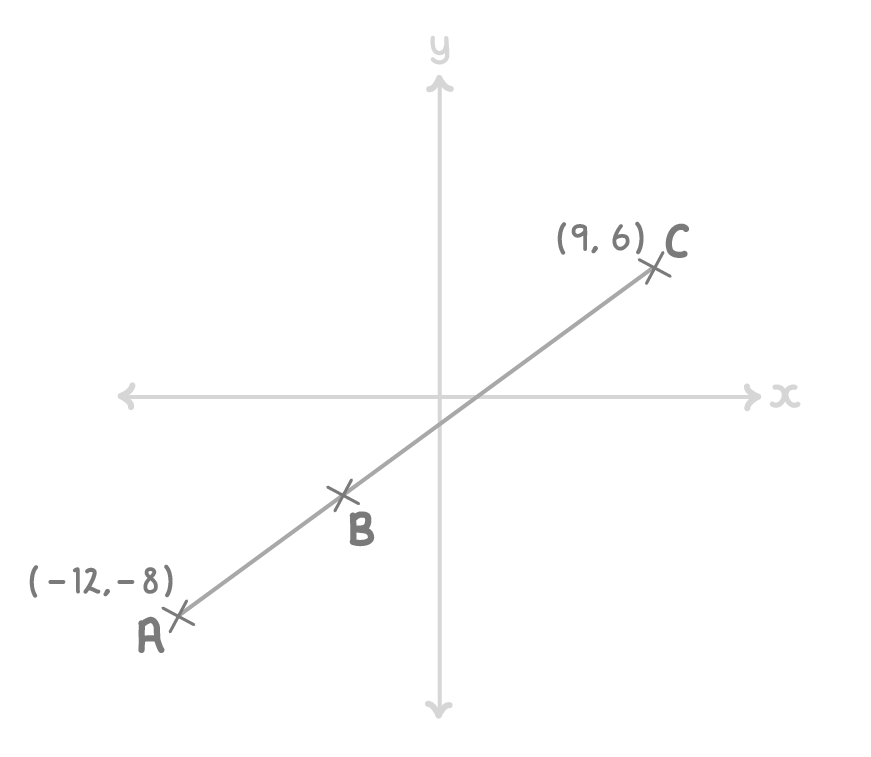
ABC is a straight line, as shown on the diagram below. AB : BC is 2 : 5.
Work out the coordinates of point B.
(Diagram NOT drawn accurately)
(-3, -2)
(-4, -6)
(-6, -4)
|
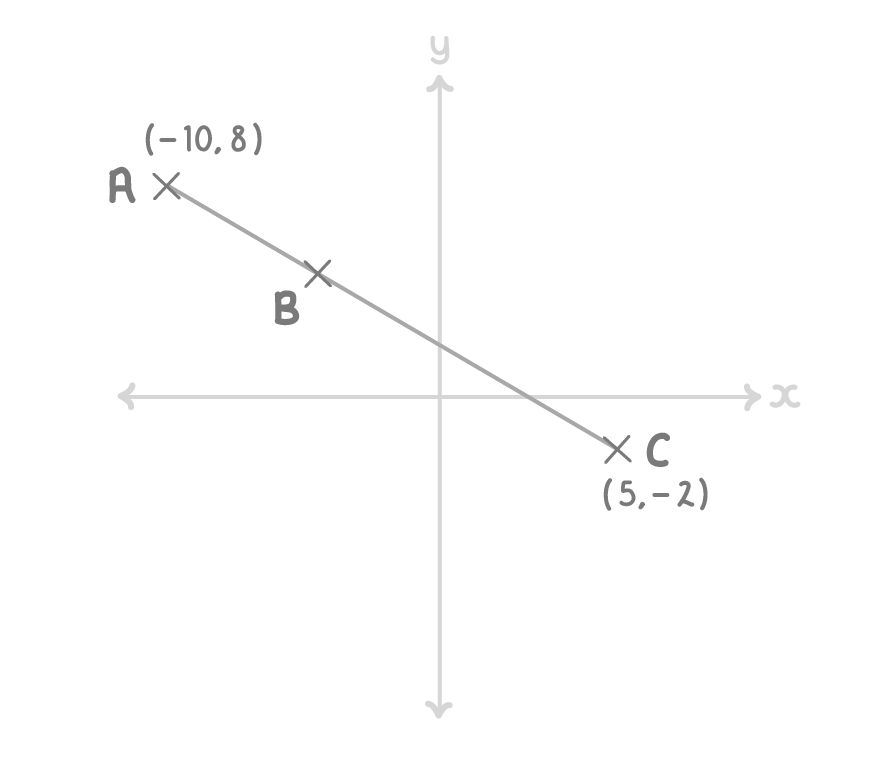
ABC is a straight line, as shown on the diagram below. AB : BC is 2 : 3.
Work out the coordinates of point B.
(Diagram NOT drawn accurately)
(3, 4)
(4, 6)
(-4, 4)
|
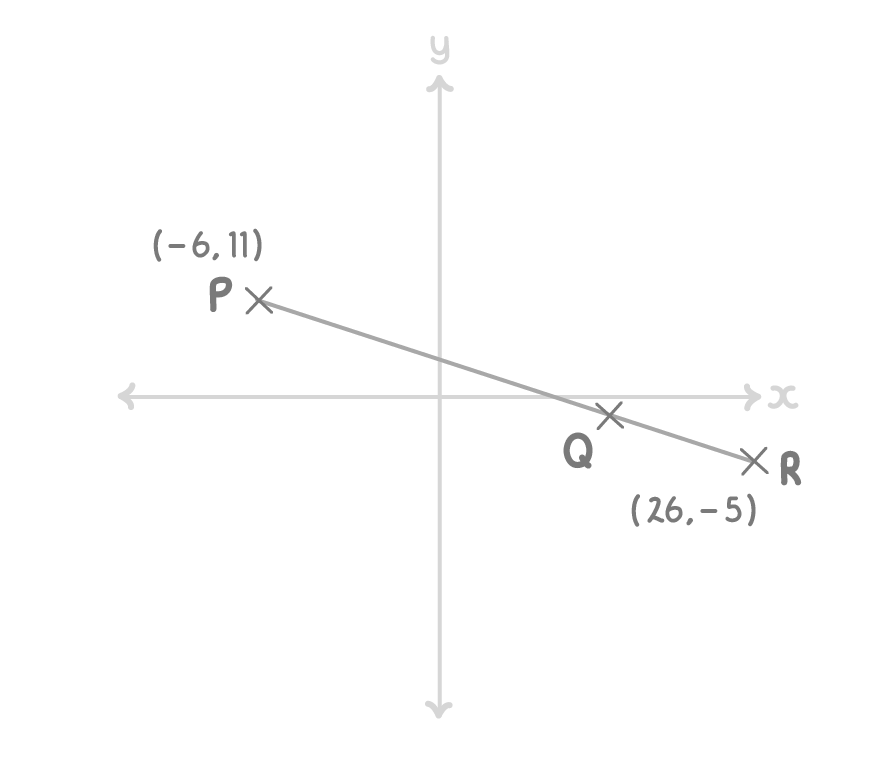
PQR is a straight line, as shown on the diagram below. PQ : QR is 3 : 1.
Work out the coordinates of point Q.
(Diagram NOT drawn accurately)
Coordinates of Q: (, )
|
Points P (-5, -2) and Q(31, -20) are joined by a straight line.
Point R is a point on PQ. PR : RQ is 7 : 2.
Work out the coordinates of point R.
(, )
|