Evaluating & Combining Functions

This lesson covers: 

  1. Understanding composite functions
  2. The process of combining two functions, f(x) and g(x), into one

What are composite functions?


Composite functions take the output of one function and use it as the input for another function.


f(g(x)) means the output of g(x) is used as the input of the f(x) function.

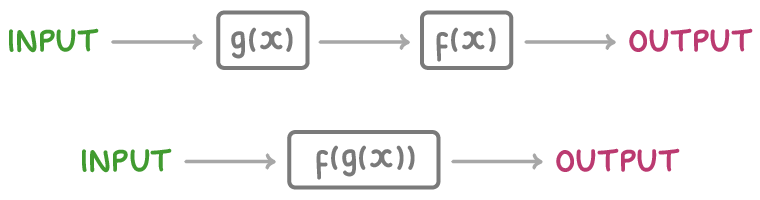
Diagram showing composite functions with input, g(x), f(x), and output.

Key points to remember:

  • The function nearest to (x) is applied first.
  • f(g(x)) is not the same as g(f(x)).

Building composite functions


To form a composite function, you replace the inner function's input with its corresponding expression before applying the outer function.


The steps are as follows:

  1. Write out the equation of the inner function.
  2. Substitute the inner function into the outer function.
  3. Simplify the composite function.
  4. To evaluate the composite function, plug in a value of x.

Worked example 1: Building composite functions


Write out the function f(g(x)), given that

f(x) = 2x - 10

g(x) = −2x​


Worked example 2: Building composite functions


Write out the function g(f(x)), given that

f(x) = 3x + 6

g(x) = 4x 

Worked example 3: Evaluating composite functions


Write out the value of  the function f(g(x)) when x = 3, given that

f(x) = 2x - 4

g(x)= 3x 

Calculate the value of g(f(x)) when x = 4, given that


f(x) = 3x + 9

g(x) = 2x

42

0

/

1

Calculate the value of g(f(x)) when x = 2, given that


f(x) = 6x + 3

g(x) = 4x

60

0

/

1

Find fg(x).


f(x) = x + 2

g(x) = x − 31​

x − 3x − 3​
2x − 3​
2x + 5x − 3​
x − 32x − 5​

0

/

1

Find ff(x).


f(x) = 2x - 4

ff(x) = 4x - 12

ff(x) = 4x2 - 8x + 16

ff(x) = 4x2 + 8

ff(x) = 4x - 8

0

/

1