The Gaseous State
This lesson covers:
- The arrangement of particles in solids, liquids and gases
- Origin of gas pressure
- The kinetic theory of gases
- The ideal gas equation
- Limitations of the ideal gas laws
Arrangement of particles in solids, liquids and gases
The properties of solids, liquids and gases depend on how the particles are arranged:
- In a solid, particles are packed closely together in a regular structure. This gives solids a high density and makes them difficult to compress. The particles vibrate about fixed positions and cannot move freely.
- In a liquid, particles can move around freely but are still fairly close together. Liquids have similar densities to solids and are also difficult to compress.
- In gases, particles have much more energy and are separated by large distances. This gives gases low density and high compressibility. The fast-moving particles can diffuse rapidly to fill a container.
The arrangement of particles and properties in solids, liquids, and gases is summarised in the table below.
| State | Particle arrangement | Particle motion | Properties |
|---|---|---|---|
| Solid | Closely packed, organised structure | Vibrate about fixed positions | High density, hard to compress |
| Liquid | Particles can move around freely, still close together | Random motion | Similar density to solids, hard to compress |
| Gas | Particles have lots of energy and large separations | Rapid, random motion | Low density, highly compressible |
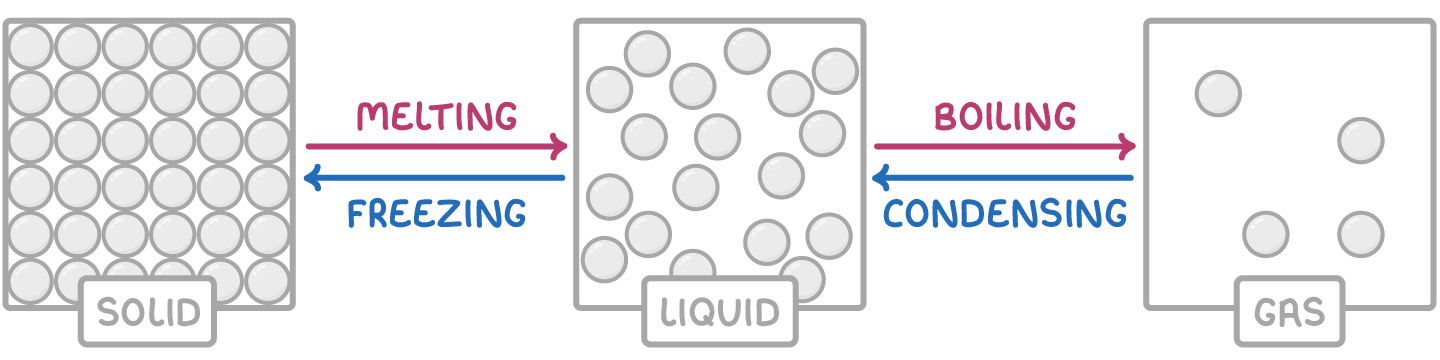
To turn a solid into a liquid or a liquid into a gas, energy must be provided, usually in the form of heating. This breaks the attractions between particles, giving them freedom to move.
Origin of pressure in gases
Gas pressure results from collisions of its particles with the container walls. These particles move randomly and rapidly, frequently hitting the walls and transferring momentum, creating a force. This force over the container's surface area is perceived as gas pressure.
Kinetic theory of gases
The kinetic theory describes the constant motion of gas particles with the following assumptions:
- Gas particles move rapidly and randomly.
- The volume of the actual gas particles is negligible compared to empty space between them.
- There are no intermolecular attractions or repulsions.
- Collisions between particles are elastic - no energy is lost.
- Temperature relates to the average kinetic energy of particles.
A hypothetical gas obeying all these assumptions is called an ideal gas.
The ideal gas equation
The ideal gas equation calculates moles of gas using pressure (p), volume (V), temperature (T) and the gas constant (R):
pV = nRT
Where:
- p = pressure (Pa)
- V = volume (m3)
- n = moles of gas
- R = the gas constant, 8.31 J K−1 mol−1
- T = temperature (K)
Worked example 1 - Calculating the volume of an ideal gas
A sealed container holds 0.150 moles of an ideal gas at a pressure of 120 kPa and a temperature of 358 K.
Calculate the volume of the container in m3.
The gas constant R = 8.31 J K−1 mol−1.
Step 1: Conversion of kPa into Pa
To convert from kPa into Pa, multiply by 1,000
120 kPa = 120,000 Pa
Step 2: Rearrange ideal gas equation
V=pnRT
Step 3: Substitution and correct evaluation
V =120,0000.150×8.31×358=3.72×10−3 m3
Worked example 2 - Calculating relative molecular mass of an ideal gas
A sealed container with a volume of 1,100 cm³ is filled with 3.18 g of an ideal gas at a temperature of 60.0°C and a pressure of 250 kPa.
Calculate the relative molecular mass (Mr) of the gas.
The gas constant R = 8.31 J K-1 mol-1
Step 1: Conversion of °C into K
To convert from °C into K, add 273
60.0°C = 333.0 K
Step 2: Conversion of cm3 into m3
To convert from cm3 into m3, divide by 1,000,000
1,100 cm3 = 1.100 x 10-3 m3
Step 3: Conversion of kPa into Pa
To convert from kPa into Pa, multiply by 1,000
250 kPa = 250,000 Pa
Step 4: Rearrange ideal gas equation
n =RTpV
Step 5: Substitution and correct evaluation
n =8.31×333.0250,000×1.100×10−3 = 0.0994 mol
Step 6: Calculate relative molecular mass
Mr =nm=0.09943.18=32.0 g mol−1
Therefore, the relative molecular mass is 32.0
Limitations of ideal gas laws
Experiments show real gases do not always follow the ideal gas predictions perfectly.
This discrepancy arises from two main factors:
- Intermolecular attractions exist between particles
- The volume of the actual gas particles cannot be ignored
These limitations are most noticeable under extreme conditions of high pressure and low temperature because:
- Gas particles are pushed very close together, allowing intermolecular attractions to become significant.
- The particle volume occupies a larger fraction of the total volume.
This makes real gases occupy smaller volumes and exert lower pressures than an ideal gas would. However, noble gases like helium and neon come close to ideal gas behaviour because their intermolecular forces are minimal.