Enthalpy Changes of Solution
This lesson covers:
- The enthalpy changes involved in dissolving ionic compounds
- Defining enthalpy changes of hydration and solution
- How to calculate enthalpy change of solution using Born-Haber cycles
Dissolving involves enthalpy changes
When an ionic solid dissolves in water, two key processes occur:
- Breaking bonds in the ionic lattice - The ionic bonds are broken to form gaseous ions. This process is endothermic and the enthalpy change is equal in magnitude but opposite in sign to the lattice enthalpy.
- Forming bonds between ions and water - New bonds form between the gaseous ions and water molecules to form hydrated ions. This process is exothermic and the enthalpy change is called the enthalpy of hydration.
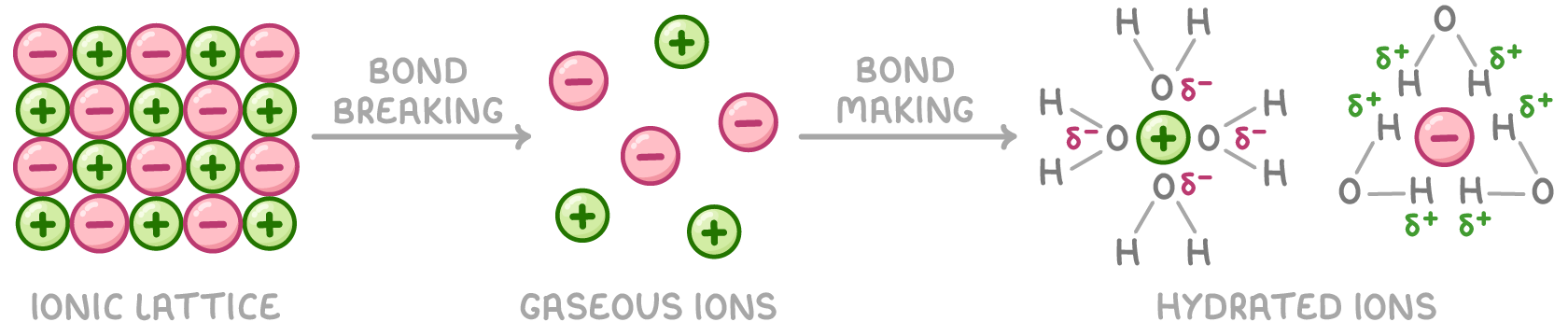
The overall enthalpy change when an ionic solid dissolves is called the enthalpy change of solution (ΔH⦵sol). It is the sum of the endothermic lattice breaking and exothermic hydration steps.
Defining enthalpy change of hydration and solution
- Enthalpy change of hydration (ΔH⦵hyd) - The enthalpy change when 1 mole of aqueous ions is formed from 1 mole of gaseous ions. For example:
Li+(g) ➔ Li+(aq)
ΔH⦵hyd values are always exothermic as energy is released when the ions become surrounded by water molecules, forming ion-dipole interactions.
- Enthalpy change of solution (ΔH⦵sol) - The enthalpy change when 1 mole of solute is dissolved in sufficient water to form a very dilute solution. For example:
LiCl(s) ➔ LiCl(aq)
ΔH⦵sol values can be either exothermic or endothermic, depending on the balance between the energy required to break the bonds in the solute and the energy released from the formation of new solute-solvent interactions.
For a substance to dissolve, the energy released from hydration must be similar to or greater than the energy required to break up the lattice. Therefore, soluble substances usually have exothermic enthalpies of solution.
Calculations involving enthalpy changes of solution and hydration
The enthalpy change of solution can be calculated using a modified Born-Haber cycle.
The key information needed is:
- The lattice enthalpy of the ionic compound
- The enthalpies of hydration for the individual gaseous ions
The enthalpy change of solution (ΔHsol) can be calculated using the formula:
ΔHsol = -ΔHlatt + ΔHhyd
Worked example 1 - Calculating the enthalpy change of solution for lithium chloride
Calculate the enthalpy change of solution for lithium chloride (LiCl) using the following data:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Lattice enthalpy of LiCl, ∆Hlatt | -853 |
| Enthalpy of hydration for Li+, ∆Hhyd(Li+) | -520 |
| Enthalpy of hydration for Cl-, ∆Hhyd(Cl-) | -364 |
Step 1: Apply Hess's law for the Born-Haber cycle
The overall enthalpy change of solution of LiCl can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
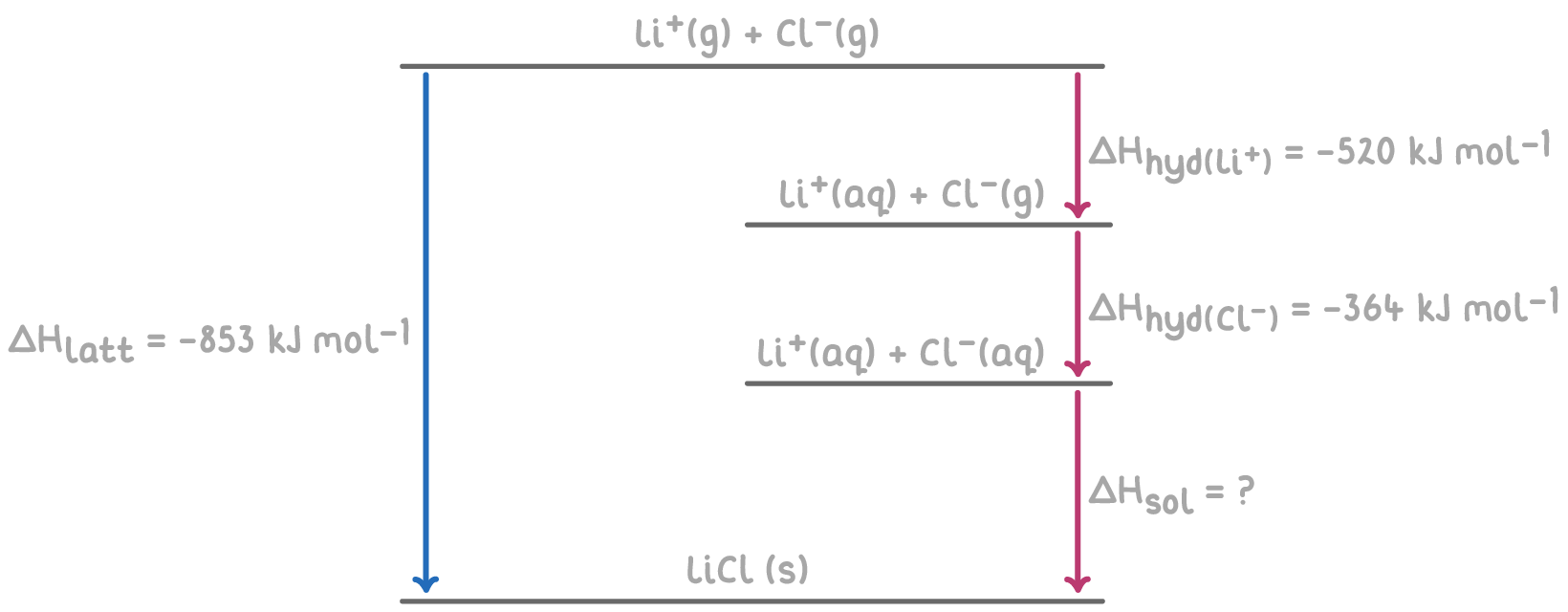
Step 2: Equation
ΔHsol = -ΔHlatt + (ΔHhyd(Li+) + ΔHhyd(Cl-))
Step 3: Substitution and correct evaluation
ΔHsol = -(-853) + ((-520) + (-364))
= 853 - 884
ΔHsol = -31 kJ mol-1
The negative value indicates that dissolving LiCl in water is exothermic, explaining why LiCl dissolves readily in water.
Worked example 2 - Calculating the enthalpy change of solution for silver chloride
Calculate the enthalpy change of solution for silver chloride (AgCl) using the following data:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Lattice enthalpy of AgCl, ∆Hlatt | -905 |
| Enthalpy of hydration for Ag+, ∆Hhyd(Ag+) | -464 |
| Enthalpy of hydration for Cl-, ∆Hhyd(Cl-) | -364 |
Step 1: Apply Hess's law for the Born-Haber cycle
The overall enthalpy change of solution of AgCl can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
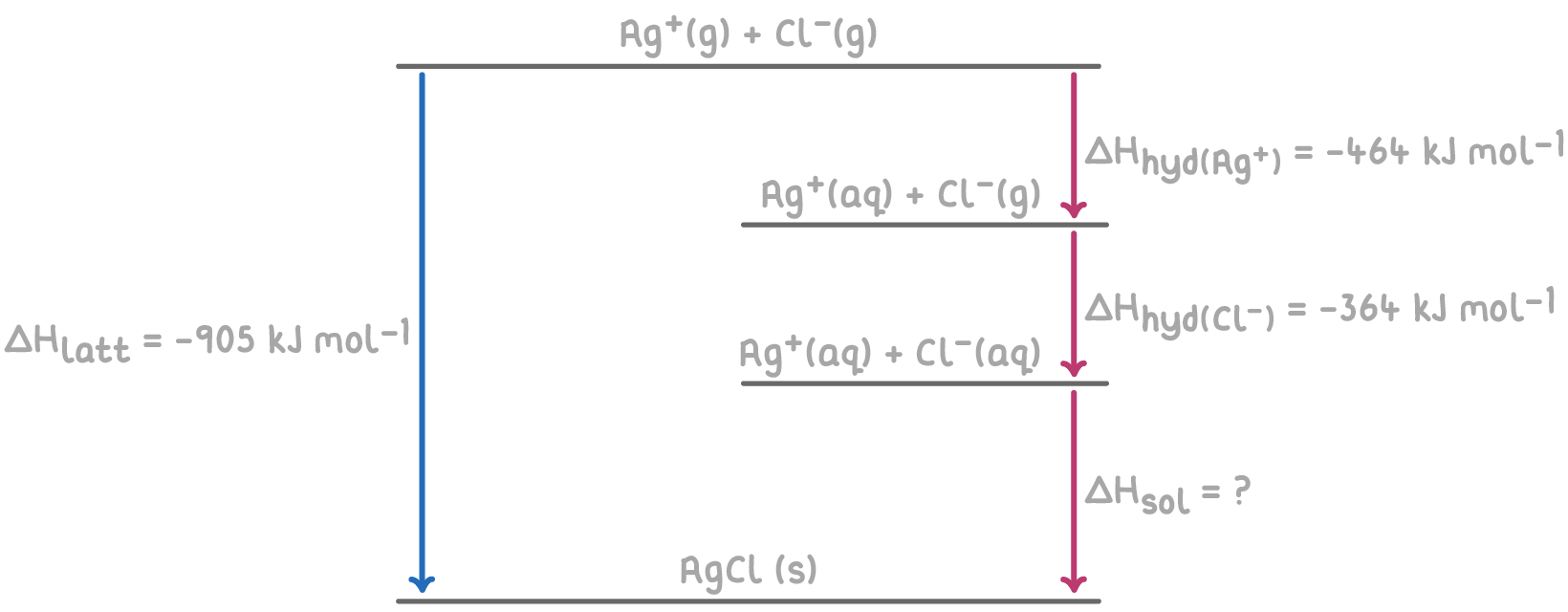
Step 2: Equation
ΔHsol = -ΔHlatt + (ΔHhyd(Ag+) + ΔHhyd(Cl-))
Step 3: Substitution and correct evaluation
ΔHsol = -(-905) + ((-464) + (-364))
= 905 -828
ΔHsol = +77 kJ mol-1
The positive value of +77 kJ mol-1 for the enthalpy change of solution indicates that dissolving AgCl in water is much less energetically favourable compared to LiCl, explaining why AgCl is insoluble in water.
Worked example 3 - Calculating the enthalpy of hydration of the Mg2+ ion
Calculate the enthalpy change of hydration for the magnesium ion (Mg2+) using the following data:
| Enthalpy change | Value (kJ mol-1) |
|---|---|
| Lattice enthalpy of MgCl2, ∆Hlatt | -2,524 |
| Enthalpy of solution of MgCl2, ∆Hsol | -160 |
| Enthalpy of hydration for Cl-, ∆Hhyd(Cl-) | -364 |
Step 1: Double the hydration enthalpy for chlorine
As MgCl2 contains two chloride ions, we need to double the enthalpy of hydration for Cl-:
- 2 x ΔHhyd(Cl-) = 2 x (-364) = -728 kJ mol-1
Step 2: Apply Hess's law for the Born-Haber cycle
The overall enthalpy change of hydration of Mg2+ can be calculated by summing the enthalpy changes for each step of the Born-Haber cycle.
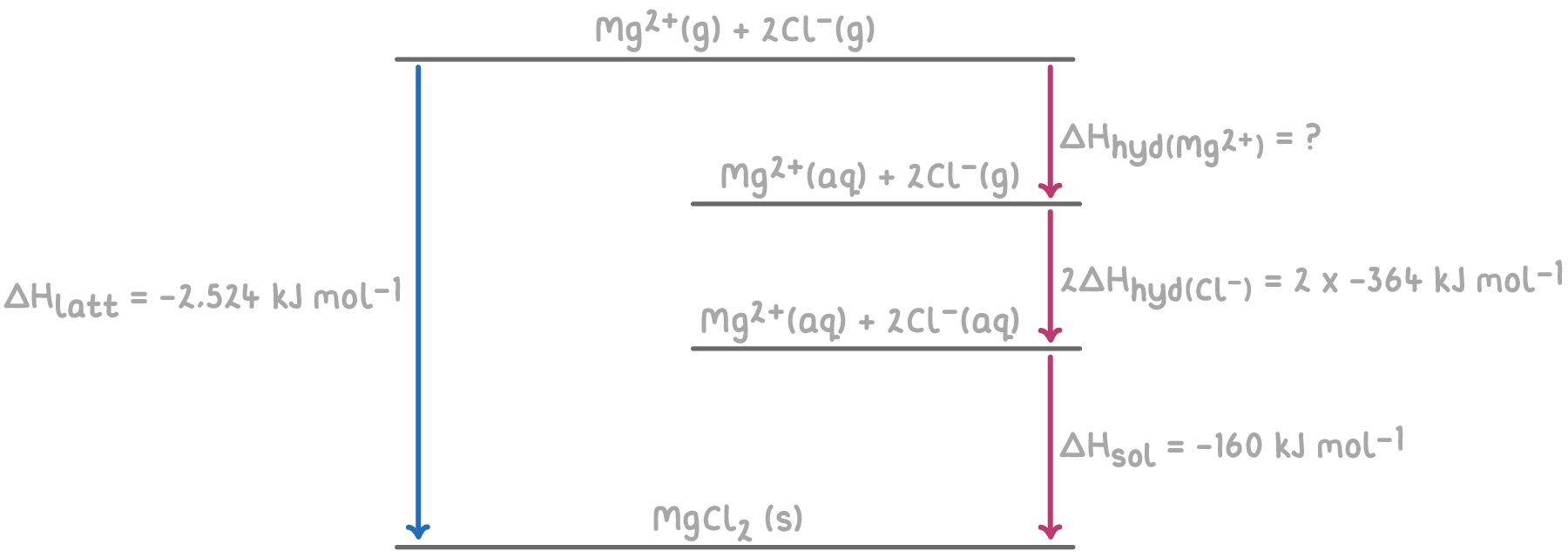
Step 3: Equation
ΔHsol = -ΔHlatt + (ΔHhyd(Mg2+) + 2ΔHhyd(Cl-))
Step 4: Rearrange equation
ΔHhyd⦵(Mg2+) = ΔHsol + ΔHlatt - 2ΔHhyd(Cl-)
Step 4: Substitution and correct evaluation
ΔHhyd(Mg2+) = (-160) + (-2,524) - (-728)
= -160 - 2,524 + 728
ΔHhyd(Mg2+) = -1,956 kJ mol-1
Therefore, the enthalpy of hydration for the Mg2+ ion is -1,956 kJ mol-1, indicating a highly exothermic process as energy is released when Mg2+ ions are hydrated by water molecules.