The Ideal Gas Equation

This lesson covers: 

  1. The kinetic theory of gases
  2. The ideal gas equation

Kinetic theory of gases

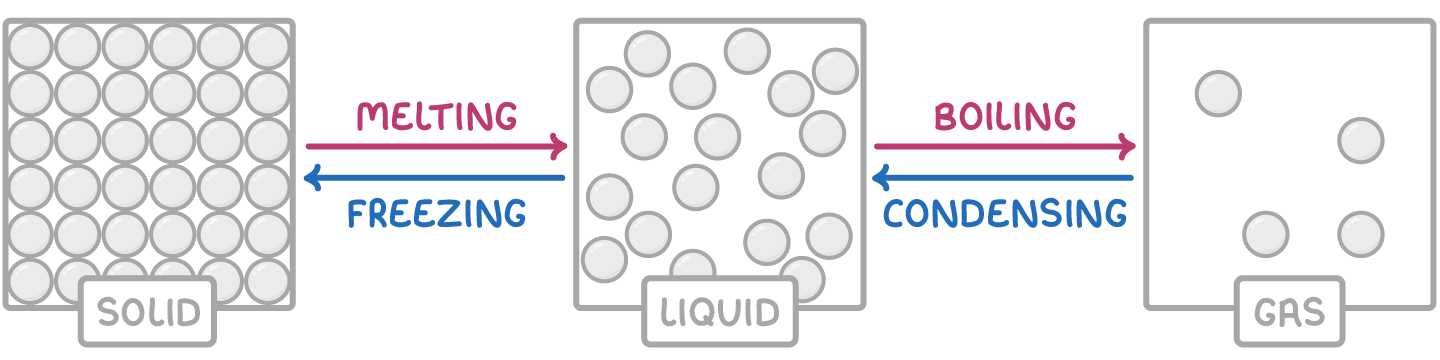
Diagram showing the transitions between solid, liquid, and gas states including melting, freezing, boiling, and condensing.

The kinetic theory describes the constant motion of gas particles with the following assumptions:

  1. Gas particles move rapidly and randomly.
  2. The volume of the actual gas particles is negligible compared to empty space between them.
  3. There are no intermolecular attractions or repulsions.
  4. Collisions between particles are elastic - no energy is lost.
  5. The average kinetic energy of particles depends only on their temperature.


A hypothetical gas obeying all these assumptions is called an ideal gas.


In reality, real gases deviate slightly from this model because real gas particles have small intermolecular attractions and non-negligible volumes, unlike the assumptions for an ideal gas.

However, noble gases like helium and neon come close to ideal behavior because their intermolecular forces are minimal.

The ideal gas equation

The ideal gas equation calculates moles of gas using pressure (p), volume (V), temperature (T) and the gas constant (R):


pV = nRT


Where:

  • p = pressure (Pa)
  • V = volume (m3)
  • n = moles of gas
  • R = the gas constant, 8.31 J K−1 mol−1
  • T = temperature (K)

Worked example 1 - Calculating the volume of an ideal gas

A sealed container holds 0.150 moles of an ideal gas at a pressure of 120 kPa and a temperature of 358 K.

Calculate the volume of the container in m3.

The gas constant R = 8.31 J K−1 mol−1.


Step 1: Conversion of kPa into Pa

To convert from kPa into Pa, multiply by 1,000

120 kPa = 120,000 Pa


Step 2: Rearrange ideal gas equation

V=pnRT​


Step 3: Substitution and correct evaluation

V =120,0000.150×8.31×358​=3.72×10−3 m3

Worked example 2 - Calculating relative molecular mass of an ideal gas

A sealed container with a volume of 1,100 cm³ is filled with 3.18 g of an ideal gas at a temperature of 60.0°C and a pressure of 250 kPa.

Calculate the relative molecular mass (Mr) of the gas.

The gas constant R = 8.31 J K-1 mol-1


Step 1: Conversion of °C into K

To convert from °C into K, add 273

60.0°C = 333.0 K


Step 2: Conversion of cm3 into m3

To convert from cm3 into m3, divide by 1,000,000

1,100 cm3 = 1.100 x 10-3 m3


Step 3: Conversion of kPa into Pa

To convert from kPa into Pa, multiply by 1,000

250 kPa = 250,000 Pa


Step 4: Rearrange ideal gas equation

n =RTpV​


Step 5: Substitution and correct evaluation 

n =8.31×333.0250,000×1.100×10−3​ = 0.0994 mol


Step 6: Calculate relative molecular mass

Mr ​=nm​=0.09943.18​=32.0 g mol−1

Therefore, the relative molecular mass is 32.0