Hess' Law

This lesson covers: 

  1. What Hess' law states
  2. How reaction enthalpies can be calculated using enthalpies of formation
  3. How reaction enthalpies can be calculated using enthalpies of combustion

Hess' law says route doesn't affect ΔH

Hess' law states that the overall standard enthalpy change (ΔH⦵) of a reaction is the same, regardless of whether the reaction takes place in one step or several steps.

This allows you to break a reaction into component steps and add up their enthalpy changes to find the total ΔH⦵ for the overall reaction.

Using enthalpies of formation

Standard enthalpies of formation (ΔH⦵f) can be used with Hess' law to determine unknown ΔH⦵ values. 

  • ΔH⦵f values are known for many compounds
  • ΔH⦵f for elements in their standard states is defined as 0 kJ mol−1


To calculate the standard enthalpy change of a reaction (ΔH⦵r), use the equation:

ΔH⦵r = ΣΔH⦵f(products) - ΣΔH⦵f(reactants)

where Σ = sum of

Worked example 1 - Calculating ΔH⦵ using enthalpy of formation data

Calculate ΔH⦵r for the reaction:

SO2(g) + 2H2S(g) ➔ 3S(s) + 2H2O(l)


Given:

ΔH⦵f(SO2(g) = -297 kJ mol-1

ΔH⦵f(H2S(g)) = -20.2 kJ mol-1

ΔH⦵f(H2O(l)) = -286 kJ mol-1

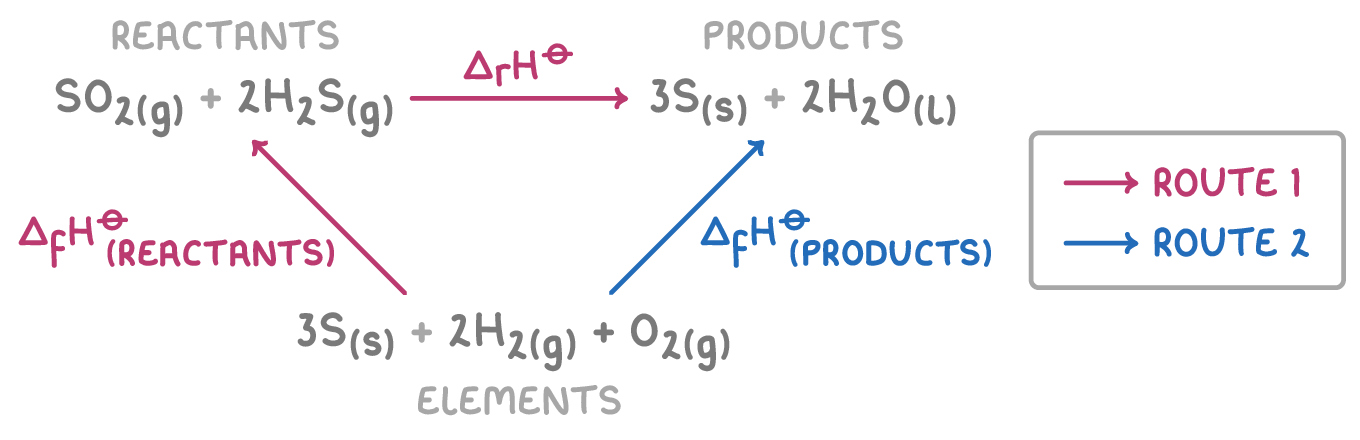
Diagram showing the reaction pathway from reactants SO2 and H2S to products S and H2O, using Hess' law to calculate ΔH.

This diagram shows the reaction pathway from reactants to products. We can use Hess' law and known enthalpy values to calculate ΔH⦵ for this reaction.



Step 1: Equation

ΔH⦵r = ΣΔH⦵f(products) - ΣΔH⦵f(reactants)


Step 2: Substitution and correct evaluation

ΔH⦵f(products) = 3(0) + 2(-286) = -572 kJ mol-1

ΔH⦵f(reactants) = -297 + 2(-20.2) = -337.4 kJ mol-1


Step 3: Determine the overall ΔH⦵

ΔH⦵ = -572 + 337.4 = -234.6 kJ mol-1

Therefore, the ΔH⦵ for the reaction is -235 kJ mol-1

Using enthalpies of combustion

In a similar way, standard enthalpies of combustion can be used to find unknown ΔH⦵r values for reactions.

To calculate the standard enthalpy change of a reaction (ΔH⦵r), use the equation:

ΔH⦵r = ΣΔH⦵c(reactants) - ΣΔH⦵c(products)

where Σ = sum of

Worked example 2 - Calculating ΔH⦵ using enthalpy of combustion data

Calculate ΔH⦵r for the reaction:

C2H5OH(l) + 3O2(g) ➔ 2CO2(g) + 3H2O(l)


Given:

ΔH⦵c(C2H5OH) = -1,367 kJ mol−1

ΔH⦵c(C) = -394 kJ mol−1

ΔH⦵c(H2) = -286 kJ mol−1

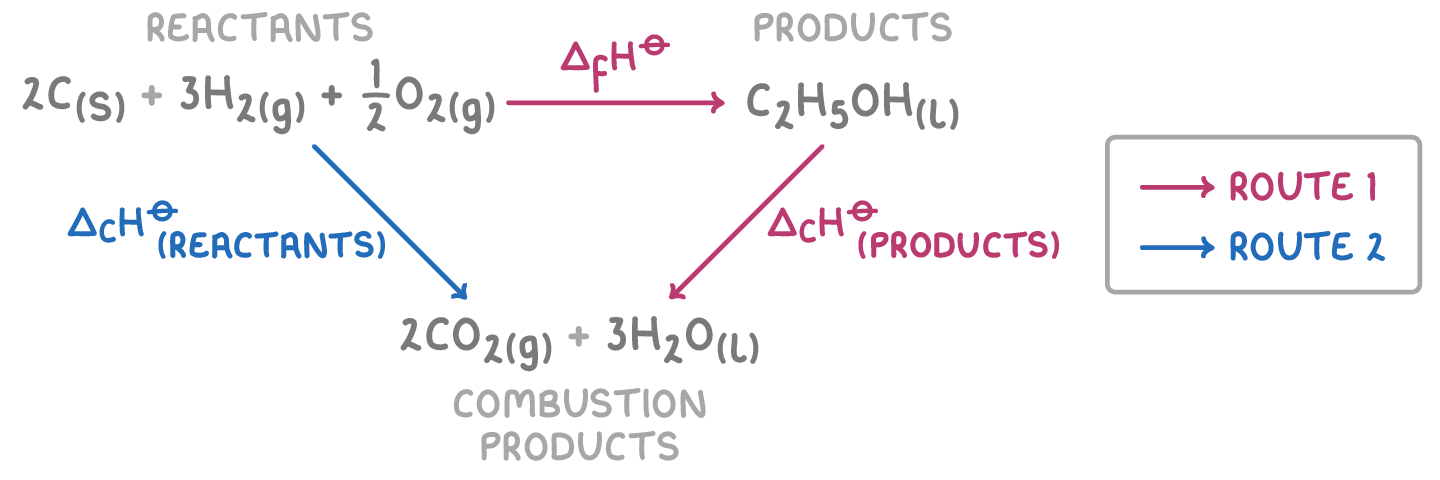
Diagram showing the reaction pathway for calculating enthalpy change using Hess' law with reactants and products.

This diagram shows the reaction pathway from reactants to products. We can use Hess' law and known enthalpy values to calculate ΔH⦵ for this reaction.



Step 1: Equation

ΔH⦵r = ΣΔH⦵c(reactants) - ΣΔH⦵c(products)


Step 2: Substitution and correct evaluation

ΔH⦵c(reactants) = 2(-394) + 3(-286) = -1,646 kJ mol-1

ΔH⦵c(products) = -1,367 kJ mol-1


Step 3: Determine the overall ΔH⦵

ΔH⦵ = -1,646 - (-1,367) = -279 kJ mol-1

Therefore, the ΔH⦵ for the formation of ethanol is -279 kJ mol-1.